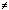Development of Parallel Methods For a 1024-Processor Hypercube*
John L. GUSTAFSON, Gary R. MONTRY, and Robert E. BENNER
Sandia National Laboratories, Albuquerque, New Mexico
March 1988
As printed in SIAM Journal on Scientific and Statistical Computing
Vol. 9, No. 4, July 1988, pp. 609-638.
(Minor revisions have been made for the Web page presentation of this paper. JLG 1995)
EDITOR'S NOTE
[This paper] reports on the research that was recognized by two awards, the Gordon Bell Award and the Karp Prize, at IEEE's COMPCON 1988 meeting in San Francisco on March 2.
The Gordon Bell Award recognizes the best contributions to parallel processing, either speedup or throughput, for practical, full-scale problems. Two awards were proposed by Dr. Bell: one for the best speedup on a general-purpose computer and a second for the best speedup on a special-purpose architecture. This year the two awards were restructured into first through fourth place awards because of the nature of the eleven December 1987 submissions. Bell presented the first place award of $1,000 to the authors of [this paper].
Following the Second Conference in Parallel Processing in November 1985, Dr. Alan Karp challenged the scientific community to demonstrate a speedup of at least 200 for a real scientific application on a general-purpose, MIMD computer. At COMPCON, Karp presented the authors with a plaque and his $100 check (to a charity of their choice) in recognition of their achievement.
The editors of SISSC are very pleased to publish this paper for many reasons. First, of course, is the natural interest in work that achieves such a high degree of parallelism for important problems. Second, the editors believe that this paper will provide the reader unfamiliar with parallel computing with an excellent overview of the issues one confronts when considering the use of a parallel architecture. Third, this paper is well written and makes its content easily accessible to the reader. For this reason, the editors have decided to publish this paper in its entirety and as rapidly as possible, though it is broader in scope and longer than those that typically appear in SISSC. It was received on March 10, revised and resubmitted on March 25.
C. W. Gear
Managing Editor, SISSC
*Received by the editors March 10, 1988; accepted for publication (in revised form) March 25, 1988. This work was performed at Sandia National Laboratories, which is operated for the U.S. Department of Energy under contract number DE-AC04-76DP00789, and partially supported by the U.S. Department of Energy's Office of Energy Research.
Abstract.
We have developed highly efficient parallel solutions for three practical, full-scale scientific problems: wave mechanics, fluid dynamics, and structural analysis. Several algorithmic techniques are used to keep communication and serial overhead small as both problem size and number of processors are varied. A new parameter, operation efficiency, is introduced that quantifies the tradeoff between communication and redundant computation. A 1024-processor MIMD ensemble is measured to be 502 to 637 times as fast as a single processor when problem size for the ensemble is fixed, and 1009 to 1020 times as fast as a single processor when problem size per processor is fixed. The latter measure, denoted scaled speedup, is developed and contrasted with the traditional measure of parallel speedup. The scaled-problem paradigm better reveals the capabilities of large ensembles, and permits detection of subtle hardware-induced load imbalances (such as error correction and data-dependent MFLOPS rates) that may become increasingly important as parallel processors increase in node count. Sustained performance for the applications is 70 to 130 MFLOPS, validating the massively parallel ensemble approach as a practical alternative to more conventional processing methods. The techniques presented appear extensible to even higher levels of parallelism than the 1024-processor level explored here.
Key words. fluid dynamics, hypercubes, MIMD machines, multiprocessor performance, parallel computing, structural analysis, supercomputing, wave mechanics
AMS(MOS) subject classifications. 65W05, 68M20, 68Q05, 68Q10
1. Introduction.
We are currently engaged in research [5] to develop new mathematical methods, algorithms, and application programs for execution on massively parallel systems. In this paper, massive parallelism refers to general-purpose Multiple-Instruction, Multiple-Data (MIMD) systems with 1000 or more autonomous floating-point processors, rather than Single-Instruction, Multiple-Data (SIMD) systems of one-bit processors such as the Goodyear MPP or Connection Machine.
The suitability of parallel architectures, such as hypercubes [20], of up to 64 processors has been demonstrated on a wide range of applications [5, 9, 10, 13, 14, 16]. The focus here is on the 1024-processor environment, which is very unforgiving of old-fashioned serial programming habits. The large number of processors forces one to reexamine every sequential aspect of a program. It also leads one to reexamine the traditional paradigm for measuring parallel processor performance.
In this paper, we examine the relationship between Amdahl's law [1] and two models of parallel performance [12]. We note that it can be much easier to achieve a high degree of parallelism than one might infer from Amdahl's law. It is often stated that production scientific programs have a substantial (several percent) inherent serial component s that limits the usefulness of the parallel approach to an asymptotic speedup of 1/s. Our results indicate that this is not necessarily the case. First, we show that s can be made quite small on practical problems through a variety of techniques that reduce non-overlapped communication, load imbalance, message startup time, and sequential operation dependency. Second, we note that when problem size is scaled in proportion to the number of processors, s can decrease, removing the barrier to speedup as the number of processors is increased.
We present massively parallel algorithms that achieve very high parallel efficiencies (98.7 percent or better) on three production scientific applications. The applications are wave mechanics using explicit finite differences, fluid dynamics of an unstable flow using the Flux Corrected Transport technique, and beam strain analysis using finite elements and the method of conjugate gradients. A brief explanation of the algorithms for host and node processors is given for each application. The results are shown as a function of both problem size and number of processors. When problem size is fixed, the serial component s is 0.0006 to 0.001, resulting in parallel speedups of 502 to 637. When the problems are scaled with the number of processors, the equivalent serial component drops to between 3 and ten parts per million, resulting in parallel speedups of 1009 to 1020.
In reducing the serial component to such a small number, several new sources of parallel efficiency loss become apparent that were previously masked. The focus here is on new effects of massive parallelism that have been heretofore unobserved and unimportant on systems of fewer than a thousand processors. These effects include inefficiency caused by redundant operations, spurious load imbalance (induced by hardware defects), and data-dependent MFLOPS rates. Future massively parallel hardware designs may find these new effects increasingly important as the number of processors in ensembles is increased and as the more traditional problems of parallel efficiency loss are solved.
The issues encountered in measuring parallel speedup on a 1024-processor system are presented in  2. Machine parameters specific to our hypercube system are summarized in
2. Machine parameters specific to our hypercube system are summarized in  3. A set of general algorithmic techniques used to achieve high parallel efficiency is described in
3. A set of general algorithmic techniques used to achieve high parallel efficiency is described in  4. Results for three applications on ensembles of up to 1024 processors are discussed in
4. Results for three applications on ensembles of up to 1024 processors are discussed in 
 5-7. Several advances in our understanding of parallel processing are summarized in
5-7. Several advances in our understanding of parallel processing are summarized in  8.
8.
2. Background discussion.
2.1. Amdahl's law revisited.
There is considerable skepticism regarding the viability of massive parallelism. The skepticism centers around Amdahl's law, an argument put forth by Gene Amdahl in 1967 [1] that for a program with serial work fraction s, the maximum parallel speedup obtainable is bounded by 1/s. This law has led to the assertion that the serial fraction will dominate execution time for any large parallel ensemble of processors, limiting the advantages of the parallel approach. Our experience with a 1024-processor system demonstrates that an assumption underlying Amdahl's argument may not be valid for large parallel ensembles.
If P is the number of processors, s is the amount of time spent (by a serial processor) on serial parts of the program, and p is the amount of time spent (by a serial processor) on parts of the program that can be done in parallel, then Amdahl's law gives
| (1) | Speedup = (s + p ) / (s + p / P)
|
| | = 1 / (s + p / P) |
where we have normalized total time s + p = 1. For P = 1024 this is a steep function of s near s = 0 (slope of approximately -P2), as shown in the left graph in Fig. 1.
The expression and graph are based on the implicit assumption that p is independent of P. However, one does not generally take a fixed-sized problem and run it on various numbers of processors; in practice, a scientific computing problem scales with the available processing power. The fixed quantity is not the problem size but rather the amount of time a user is willing to wait for an answer; when given more computing power, the user expands the problem (more spatial variables, for example) to use the available hardware resources.
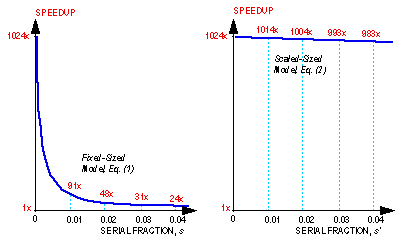
Figure 1. Speedup given by Amdahl's law and by problem scaling [12].
As a first approximation, we have found that it is the parallel part of a program that scales with the problem size. Times for program loading, serial bottlenecks, and I/O that make up the s component of the application do not scale with problem size. When we double the number of processors, we double the number of spatial variables in a physical simulation. As a first approximation, the amount of work that can be done in parallel varies linearly with the number of processors (
 5.5, 6.5, and 7.5).
5.5, 6.5, and 7.5).
We now consider the inverse of Amdahl's paradigm: rather than ask how fast a given serial program would run on a parallel processor, we ask how long a given parallel program would have taken to run on a serial processor. If we use s' and p' to represent serial and parallel time spent on the parallel system, s' + p' = 1, then a uniprocessor requires time s'+p'P to perform the task. This reasoning gives an alternative to Amdahl's law [4], [12]:
| (2) | Scaled speedup = (s' + p'P ) / (s' + p' )
|
| | = P + (1 - P) s'. |
In contrast to the curve for (1), this function is simply a line, of moderate slope 1- P, as shown in the right graph of Fig. 1. When speedup is measured by scaling the problem size, the scalar fraction s tends to shrink as more processors are used. It is thus much easier to achieve efficient parallel performance than is implied by Amdahl's paradigm, and performance as a function of P isn't necessarily bounded by an asymptote.
2.2. Fixed and scaled problem size.
Measurements of parallel performance are best displayed as a function of both problem size and ensemble size. Two subsets of this domain have received attention in the parallel processing community. The first subset we call the fixed-sized speedup line (Fig. 2). Along this line, the problem size is held fixed and the number of processors is varied. On shared-memory machines, especially those with only a few processors, this is reasonable since all processors can access memory through a network transparent to the programmer. On ensemble computers, fixing the problem size creates a severe constraint, since for a large ensemble it means that a problem must run efficiently even when its variables occupy only a small fraction of available memory.
Figure 2. Ensemble computing performance pattern.
For ensemble computers the scaled speedup line (Fig. 2) is an alternative computational paradigm. It is the line along which problem size increases with the number of processors, as discussed in the previous section. The computation-to-communication ratio is higher for scaled problems. One can model the performance of these scaled problems with a hypothetical processor node that has direct uniprocessor access to all of the real random-access memory of the machine. This hypothetical processor performance is numerically equivalent (after adjustment by a factor introduced in  2.2.1) to the ratio of measured MFLOPS rates in
2.2.1) to the ratio of measured MFLOPS rates in 
 5, 6 and 7. An example of these scaled speedup calculations is given in
5, 6 and 7. An example of these scaled speedup calculations is given in  2.2.2.
2.2.2.
2.2.1. Operation efficiency.
Conversion of an algorithm from serial to parallel often increases the operation count. For example, it might be more efficient to have each processor calculate a globally required quantity than to have one processor calculate it and then communicate it to other processors. We define  (N) to be the operation count for the best serial algorithm, where N is the size of the problem in one dimension. We also define
(N) to be the operation count for the best serial algorithm, where N is the size of the problem in one dimension. We also define  P(N) to be the total operation count for the best parallel algorithm; in general,
P(N) to be the total operation count for the best parallel algorithm; in general,  P(N)
P(N) 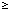
 (N). Also,
(N). Also,  1(N)
1(N) 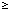
 (N), where
(N), where  1(N) is the operation count for the parallel algorithm executed on one processor. As a result, the P processors can be 100 percent busy on computation and still be less than P times faster than the best serial algorithm. For example, suppose that a two-dimensional simulation requires a serial operation count given by
1(N) is the operation count for the parallel algorithm executed on one processor. As a result, the P processors can be 100 percent busy on computation and still be less than P times faster than the best serial algorithm. For example, suppose that a two-dimensional simulation requires a serial operation count given by
| (3) |  (N) = a + bN + cN2 (N) = a + bN + cN2
|
where a, b, and c are constant nonnegative integers. In running the N-by-N problem in parallel on P processors, each processor treats a subdomain with operation cost  (N/
(N/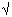 P). This operation cost is more work than would be performed by a serial processor:
P). This operation cost is more work than would be performed by a serial processor:
Equality is only possible if a = b = 0 in (3).
We define an operation efficiency factor 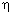 P(N) given by
P(N) given by
where  P(N) is permitted to be a general function of P. When we refer to the efficiency of a particular node, we are accounting both for the apparent efficiency (compute time divided by total time) and the operation efficiency as defined in (5). This concept can be used to tune parallel performance by providing an analytical model of the tradeoff between communication overhead and operation inefficiency. Note that an exact floating-point operation count is required to make this measurement.
P(N) is permitted to be a general function of P. When we refer to the efficiency of a particular node, we are accounting both for the apparent efficiency (compute time divided by total time) and the operation efficiency as defined in (5). This concept can be used to tune parallel performance by providing an analytical model of the tradeoff between communication overhead and operation inefficiency. Note that an exact floating-point operation count is required to make this measurement.
2.2.2. Example of scaled speedup calculation.
The WAVE program ( 5) can simulate a 6144-by-6144 gridpoint domain (192-by-192 on each of 1024 processors). This large problem requires 340 MBytes for the data structures alone, and cannot be run on a single processor. However, it is possible to measure interprocessor communication time and idle time on each processor to within a few thousandths of a second. If a 1024-processor job requires 10,000 seconds, of which 40 seconds is the average time spent by all processors doing work that would not be done by a serial processor, then one can compute efficiency for the distributed ensemble as (10,000 - 40) / 10000 = 99.6 percent. (
5) can simulate a 6144-by-6144 gridpoint domain (192-by-192 on each of 1024 processors). This large problem requires 340 MBytes for the data structures alone, and cannot be run on a single processor. However, it is possible to measure interprocessor communication time and idle time on each processor to within a few thousandths of a second. If a 1024-processor job requires 10,000 seconds, of which 40 seconds is the average time spent by all processors doing work that would not be done by a serial processor, then one can compute efficiency for the distributed ensemble as (10,000 - 40) / 10000 = 99.6 percent. (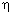 P is unity for this application.) The scaled speedup is then 0.996 x 1024
P is unity for this application.) The scaled speedup is then 0.996 x 1024 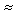 1020. An equivalent definition is the following: speedup is the sum of the individual processor efficiencies. Speedup shown in the graphs and tables in
1020. An equivalent definition is the following: speedup is the sum of the individual processor efficiencies. Speedup shown in the graphs and tables in 
 5-7 is derived this way. Alternatively, the scaled speedup can be computed as 113 MFLOPS / 0.111 MFLOPS
5-7 is derived this way. Alternatively, the scaled speedup can be computed as 113 MFLOPS / 0.111 MFLOPS 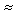 1020 (see
1020 (see  5.5).
5.5).
2.3. Practical benchmarking considerations.
There are parameters in every program that affect execution times and that are user-controllable, such as the amount of output, grid resolution, or number of timesteps. Users adjust these parameters according to their computing environment. We have endeavored in benchmarking to select values representative of production engineering activities and to include all times, both computing and overhead, associated with a job.
2.3.1. Limitations on execution time for fixed-sized speedup.
Linear speedup on 1024 processors reduces a two-minute uniprocessor execution time to 0.126 seconds, which would be barely discernible to the user because of job startup time. However, a job that requires about two minutes on 1024 processors might take 30 hours on a single processor, making it tedious to benchmark. A two-minute job on 1024 processors seems to be a reasonable upper bound for a benchmark. Moreover, when using 1024 processors, we have found that the time to complete even the most trivial computation (load all processors, do one operation, send result back to the host) is about two seconds. To achieve reasonable efficiency, we must choose a job time at least one order of magnitude greater than this fixed overhead. Hence, as a compromise for fixed-sized benchmarking we have aimed for 4 to 30 hours for the uniprocessor jobs, which results in about 20 to 200 seconds for the 1024-processor jobs. For the three applications reported herein, we choose the spatial discretization, number of timesteps, or convergence criteria to approximate these times. The selections were within the limits of what an engineer or scientist would actually choose in a production environment. However, note that for some applications of interest, several hours, even days, of execution time are not uncommon.
2.3.2. Input and output.
Each program provides the input and output (I/O) that would typically be demanded by someone using the program as a production design tool. Tables and input conditions are read from disk and keyboard; timestep history and final state go to both disk storage and to a color graphics display. The amount of I/O that can be demanded of a simulation is almost unbounded; the greater the demand, the more challenging it is to overlap I/O with computation. Eventually a penalty is paid, in both speedup and absolute performance. We choose enough I/O to provide continuous interaction with the user regarding the progress of the computation, and then the solution or final timestep. For the applications discussed here, non-overlapped I/O requires less than two seconds on any job.
3. The NCUBE parallel computer.
The NCUBE/ten is well suited for parallel speedup research. It has more processors than the maximum configuration of any other MIMD machine currently available. Since each processor has 512 KBytes of memory and a complete environment, it is possible to run a fixed-sized problem of practical size on a single processor. Each NCUBE node has fast enough 32-bit and 64-bit floating-point arithmetic for the 1024-node ensemble to be competitive with conventional supercomputers on an absolute performance basis.
All memory is distributed in the hypercube architecture. Information is shared between processors by explicit communications across I/O channels (as opposed to the shared-memory approach of storing data in a common memory). Therefore, the best parallel applications are those that seldom require communications which must be routed through nodes. The applications presented here use these point-to-point paths exclusively. The NCUBE provides adequate bandwidth for moving data to and from I/O devices such as host, disk, and graphics display. The operating system can allocate subcubes to multiple users with very little interference between subcubes. In fact, much of our benchmarking is performed while sharing the cube with various sized jobs and various applications.
3.1. Machine parameters.
The NCUBE processor node is a proprietary, custom VLSI design. It contains a complete processor (similar in architecture to a VAX-11/780 with Floating Point Accelerator), 11 bidirectional Direct Memory Access (DMA) communications channels, and an error-correcting memory interface, all on a single chip. Both 32-bit and 64-bit IEEE floating-point arithmetic are integral to the chip and to the instruction set. Each node consists of the processor chip and six 1-Mbit memory chips (512 KBytes plus error correction code).
Of relevance to this discussion is the ratio of computation time to communication time in such a processor node, as actually measured. Currently, a floating-point operation takes between 7 and 15 µseconds to execute on one node, using the Fortran compiler and indexed memory-to-memory operations (peak observed floating-point performance is 0.17 MFLOPS for assembly code kernels with double precision arithmetic). Our experience is that computationally-intensive single-node Fortran programs fall within this range (0.07 to 0.13 MFLOPS). This performance is expected to improve as the compiler matures. Integer operations are much faster, averaging a little over 1 µsecond when memory references are included.
The time to move data across a communications channel can sometimes be overlapped, either with computations or with other communications ( 4.1). However, our experience using subroutine calls from Fortran shows that a message requires about 0.35 milliseconds to start and then continues at an effective rate of 2 µseconds per byte. It is then possible to estimate just how severe of a constraint on speedup one faces when working a fixed-sized problem using 1024 processors: Suppose that an application requires 400 KBytes for variables on one node (50K 64-bit words). If distributed over 1024 processors, each node will only have 50 variables in its domain. For a typical timestepping problem, each variable might involve ten floating-point operations (120 µseconds) per timestep, for a total of 6 milliseconds before data must be exchanged with neighbors. This computational granularity excludes the effective overlap of communication with computation that is achieved for larger problems (see
4.1). However, our experience using subroutine calls from Fortran shows that a message requires about 0.35 milliseconds to start and then continues at an effective rate of 2 µseconds per byte. It is then possible to estimate just how severe of a constraint on speedup one faces when working a fixed-sized problem using 1024 processors: Suppose that an application requires 400 KBytes for variables on one node (50K 64-bit words). If distributed over 1024 processors, each node will only have 50 variables in its domain. For a typical timestepping problem, each variable might involve ten floating-point operations (120 µseconds) per timestep, for a total of 6 milliseconds before data must be exchanged with neighbors. This computational granularity excludes the effective overlap of communication with computation that is achieved for larger problems (see  6.4.1). Data exchange might involve four reads and four writes of 80 bytes each, for a worst-case time of (4 + 4) x (350 + 80 x 2) µseconds, or about 4 milliseconds. Therefore, when a single-node problem is distributed on the entire 1024-processor ensemble, the parallel overhead on the NCUBE will be about 40 percent. This estimate is validated by the experimental results presented in
6.4.1). Data exchange might involve four reads and four writes of 80 bytes each, for a worst-case time of (4 + 4) x (350 + 80 x 2) µseconds, or about 4 milliseconds. Therefore, when a single-node problem is distributed on the entire 1024-processor ensemble, the parallel overhead on the NCUBE will be about 40 percent. This estimate is validated by the experimental results presented in 
 5.5, 6.5, and 7.5. The cost of synchronization and load imbalance appears secondary to that of message transfers (for interprocessor communications and I/O) for the three applications discussed herein.
5.5, 6.5, and 7.5. The cost of synchronization and load imbalance appears secondary to that of message transfers (for interprocessor communications and I/O) for the three applications discussed herein.
3.2. Normalized arithmetic.
Even when the computation appears perfectly load balanced on the ensemble, there can be load imbalance caused by data-dependent differences in arithmetic times on each node. For example, the NCUBE processor does not take a fixed amount of time for a floating-point addition. The operands are shifted to line up their binary points at a maximum speed of two bits per clock prior to the actual addition, or normalized at a similar rate if the sum yields a number smaller than the operands. The sum of 3.14 and 3.15 executes at maximum speed, but the sum of 3.14 and 0.0003, or 3.14 and -3.15, takes additional cycles. The microprocessor also does a check, in parallel, of whether either operand is zero, and shortcuts the calculation if true. This timing variability is typical of the VAX-type architectures, but is very unlike that of machines like the CRAY that have pipelined arithmetic. Statistically, the NCUBE nodes have nearly the same amount of work to do; however, variation caused by data introduces a slight load imbalance in the large jobs.
4. General techniques.
4.1. Communication overlap.
The communications channels for each node are, in principle, capable of operating concurrently with the processor itself and with each other, up to the point where memory bus bandwidth (7.5 MByte/second) is saturated. However, the Direct Memory Access (DMA) channels are managed by software running on the processor. The software creates overhead that limits the extent to which communications can be overlapped.
Careful ordering of reads and writes can yield considerable overlap and economy, halving the time spent on interprocessor communication. As an example, Fig. 3 shows the pattern used for the two-dimensional Wave Mechanics problem ( 5); the other applications use similar techniques for nearest-neighbor communication in two dimensions.
5); the other applications use similar techniques for nearest-neighbor communication in two dimensions.
The messages sent and received in Fig. 3 are 768 bytes long. The actual DMA transfers require 1.20 µseconds per byte, or 0.9 milliseconds for each message. Before a message can be written, it is first copied to a location in system buffer memory where messages are stored in a linked-list format. For a 768-byte message, the copy and startup time for writing a message is about 0.4 milliseconds. We found it best to arrange the writes as in Fig. 3 rather than alternate writes and reads. This arrangement reduces the number of synchronizations from four to one; it also ensures, as much as possible, that messages have arrived by the time the corresponding reads are executed.
Figure 3. Overlapped communications.
When subroutine calls to read messages are issued in the same order that corresponding messages are written, the probability of an idle state (waiting for message) is reduced. Therefore, if the first write is in the "up" direction, the first read should be from the "down" direction. About 0.2 milliseconds of processor time is needed to prepare to receive the message. If there is no waiting (i.e., all connected processors are ready to write), and there is little contention for the memory bus, then the read operations proceed with overlapped DMA transfers. As shown in Fig. 3, four channels can operate simultaneously for modest message lengths even when startup overhead is taken into account. In Fig. 3, an average of 2.5 DMA channels are operating simultaneously.
After each message is read into a system buffer, it is copied back to the Fortran array so it can again be used in the program. For the 768-byte message, this requires about 0.2 milliseconds. The total time for a complete set of four writes and four reads is less than 4 milliseconds for this example. This time compares with a computation time of about 3 seconds for the interior points. Thus, with careful management, computation time can be made almost three orders of magnitude greater than parallel communication overhead.
Note also that the total transfer in Fig. 3 is 6144 bytes in 3.5 milliseconds, or 0.6 µseconds/byte; because of overlap, this is less than the theoretical time required to send 6144 bytes over one channel: 7.3 milliseconds. Hence, one cannot use simple parametric models of communication speed and computation speed to accurately predict ensemble performance.
4.2. Message gather-scatter.
In sending edge data to nearest neighbors in a two-dimensional problem, two of the four edges in the array have a non-unit stride associated with their storage. Since the communications routines require contiguous messages, it is first necessary to gather the data into a message with a Fortran loop for those two edges. The result is quadruple buffering of messages, as shown in Fig. 4.
Figure 4. Quadruple buffering.
The NCUBE Fortran compiler produces considerable loop overhead for the gather and scatter tasks, and our studies show that a hand-coded assembly routine for these tasks is actually 11 times faster than Fortran. On the parallel version of WAVE ( 5) for example, the assembly code routine is used to gather the edge data and to scatter the message back to the edge. (Figure 4 shows times using assembly code.) This change improved fixed-sized parallel speedup by as much as 20 percent.
5) for example, the assembly code routine is used to gather the edge data and to scatter the message back to the edge. (Figure 4 shows times using assembly code.) This change improved fixed-sized parallel speedup by as much as 20 percent.
4.3. Message organization.
Considerable communication time can be saved by judicious reorganization of data and computation within the application. In particular, it is very important to avoid message startup time by coalescing individual messages wherever possible. The total overhead for every message is about 0.35 milliseconds, which limits the fine-grained parallel capability of the hypercube. In spreading problems thinly across processors for the purpose of measuring fixed-sized problem speedup, message startup time dominates the parallel overhead. To mitigate this effect, we have structured the algorithms so that communications are grouped rather than alternated with computation. Data structures were organized so that successive communications can be changed into a single communication of concatenated data.
As an example, the first attempt at a hypercube version of the fluid dynamics program ( 6) descended from a vector uniprocessor version, and required over 400 nearest-neighbor read-write message pairs per timestep. Reorganization of data structures and computation reduced the nearest-neighbor communication cost to 48 message pairs per timestep. This reduction primarily involved the reorganization of dependent variable arrays into one large structure with one more dimension. The restructuring placed nearest-neighbor data into a contiguous array for two of the communicated edges, and a constant stride array on the other two edges. The constant stride arrays are gathered into a contiguous array by an optimized routine (
6) descended from a vector uniprocessor version, and required over 400 nearest-neighbor read-write message pairs per timestep. Reorganization of data structures and computation reduced the nearest-neighbor communication cost to 48 message pairs per timestep. This reduction primarily involved the reorganization of dependent variable arrays into one large structure with one more dimension. The restructuring placed nearest-neighbor data into a contiguous array for two of the communicated edges, and a constant stride array on the other two edges. The constant stride arrays are gathered into a contiguous array by an optimized routine ( 4.2) at a cost of about 0.3 µseconds per byte.
4.2) at a cost of about 0.3 µseconds per byte.
4.4. Global exchange.
Many of the kernels generally thought of as "serial" (order P time complexity for P processors) can actually be performed in log2P time using a series of exchanges across the dimensions of the cube. For example, the accumulation of inner products is performed efficiently by means of bidirectional exchanges [18] of values along successive dimensions of the hypercube, interspersed with summation of the newly-acquired values (Fig. 5). This algorithm requires the optimal number of communication steps, log2P. Note that we do not perform a "global collapse" that condenses the desired scalar to one processor which must then be broadcast to all nodes. The exchange does more computations and messages than a collapse, but requires half the passes to produce the desired sum on each processor. A similar pattern can be used to perform such "serial" operations as finding global maxima, global minima, and global sums, in time proportional to log2P rather than P.
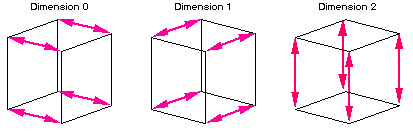
Figure 5. Global exchange for inner products.
This technique is used, for example, for the conjugate gradient iterations in the structural analysis problem to perform inner products, and in the fluid dynamics problem to establish the maximum timestep that satisfies the Courant-Friedrich-Lewy (CFL) condition. For the structural analysis problem, the time to accomplish the pattern shown in Fig. 5 for a ten-dimensional hypercube is 7.7 milliseconds, consistent with the discussion in  4.1 (ten reads, ten writes, 0.35 milliseconds startup per read or write).
4.1 (ten reads, ten writes, 0.35 milliseconds startup per read or write).
4.5. Logarithmic-cost fanout.
Fig. 6 shows the fanout algorithm [18] used to load 64 processors in an order 6 hypercube. By using a tree to propagate redundant information, the time for operations such as loading the applications program or the node operating system is greatly reduced. This pattern is used in reverse to collect output. In contrast to the global exchange technique of  4.4, the tree method is most useful when information must be sent to or received from the host.
4.4, the tree method is most useful when information must be sent to or received from the host.
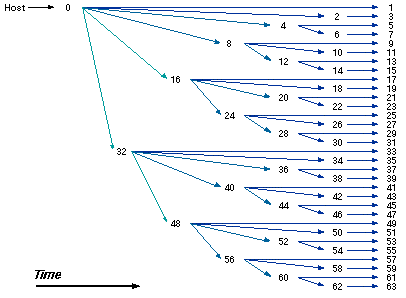
Figure 6. Logarithmic fanout.
As an example of the savings provided by this technique, a 12500-byte executable program is loaded onto a 512-node hypercube in 1.33 seconds using a pattern similar to the one shown in Fig. 6, compared with 61.18 seconds using a serial loading technique. The performance ratio is 46 to 1. For a 1024-node hypercube, the logarithmic technique is 83 times faster. The logarithmic technique can disseminate a block of 480 KBytes (the maximum user space in each node) in less than one minute, whereas the serial technique requires an hour and twenty minutes.
5. Application 1: Wave mechanics
5.1. Application description.
The WAVE program calculates the progress of a two-dimensional surface (acoustic) wave through a set of deflectors, and provides a graphic display of the resulting heavily-diffracted wavefront. The program is capable of handling reflectors of any shape (within the resolution of the discretized domain).
5.2. Mathematical formulation.
The Wave Equation is
where 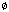 and c are functions of the spatial variables. In general,
and c are functions of the spatial variables. In general, 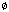 represents the deviation of the medium from some equilibrium (pressure, height, etc.) and c is the speed of wave propagation in the medium (assumed to be isotropic). For nonlinear waves, c is also a function of the wave state.
represents the deviation of the medium from some equilibrium (pressure, height, etc.) and c is the speed of wave propagation in the medium (assumed to be isotropic). For nonlinear waves, c is also a function of the wave state.
A discrete form of (6) for a two-dimensional problem on [0, 1] x [0, 1] is
| (7) | c2[F(i, j+1)+F(i, j-1)+F(i+1, j)+F(i-1, j) - 4F(i, j)] / h2 |
| | = [Fnew(i, j) - 2 F(i, j) + Fold(i, j)] / ( t)2 t)2
|
where F(i, j) =  (ih, jh), h = 1/N. Equation (7) can be rearranged into a scheme where Fnew is computed explicitly from F and Fold. Hence, only two timesteps need to be maintained in memory simultaneously ("leapfrog" method).
(ih, jh), h = 1/N. Equation (7) can be rearranged into a scheme where Fnew is computed explicitly from F and Fold. Hence, only two timesteps need to be maintained in memory simultaneously ("leapfrog" method).
There is ample literature regarding the convergence of this method [8, 15] as a function of c2, h, and  t. For example, it is necessary (but not sufficient) that (
t. For example, it is necessary (but not sufficient) that ( t)2 ² (h/c)2/ 2 (CFL condition). We use constant c and (
t)2 ² (h/c)2/ 2 (CFL condition). We use constant c and ( t)2 = (h/c)2/ 2 in our benchmark.
t)2 = (h/c)2/ 2 in our benchmark.
5.3 Test problem.
To demonstrate the capability of the algorithm, a test problem is used that included internal reflecting boundaries (Fig. 7).
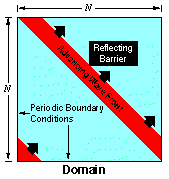
Figure 7. Wave mechanics problem.
The reflecting barrier is a rectangle that is one-sixth by one-third the domain size. A diagonal wave of width one-sixth the domain size impinges on the barrier, creating reflections and diffractions difficult to compute by analytic means. Feature proportions of one-sixth and one-third allow discretizations as coarse as 6-by-6 for the domain to correspond in a simple way to discretizations of size 12-by-12, 24-by-24, and so forth.
5.4. Parallel algorithm.
ALGORITHM a
Host Program for the Wave Mechanics Problem
a1. [Start.] Prompt the user for the desired hypercube dimension. For simplicity, we require that the dimension be even so that grid resolution always scales in both dimensions.
a2. [Open subcube.] Open the requested hypercube, and send a copy of the WAVE node program (Algorithm A) to all nodes using a logarithmic fanout. (Nodes begin execution and start timing their job as soon as they are loaded.)
a3. [Determine problem size.] Prompt the user for the desired resolution of the discretization, and the desired number of timesteps. (The resolution can be N = 6, 12, 24, 48, 96, or 192 per node; the number of timesteps must be even.) Send both parameters to every node.
a4. [Prepare for node output.] While the first timestep is being calculated, initialize the graphics display (load color table, clear screen, compute scale factors), and determine the gray code mapping of nodes to the two-dimensional domain.
a5. [Read timestep.] If the "History" flag is true, read the timestep data from each node (pixel values, 0 to 255) and display on the graphics monitor. (Sending pixels instead of floating-point values saves message length and host effort.)
a6. [Next timestep.] Repeat step a5 for every timestep.
a7. [Read last timestep.] Read the final timestep data from each node and display it (regardless of the state of the "History" flag).
a8. [Read timers.] Read the timing data from every node. Find the minimum and maximum processor times, compute MFLOPS, and display on the ASCII monitor. (The computation of application MFLOPS is the only floating-point arithmetic performed by the host algorithm.)
a9. Close the allocated hypercube.
ALGORITHM A
Node Program for the Wave Mechanics Problem
A1. [Start timer.] Prior to any other executable statement, execute a system call to record the time.
A2. [Obtain node location.] Execute a system call to obtain this node's processor number (0 to 1023, gray code) and the dimension of the cube.
A3. [Find gray code mapping.] Use the data from step A2 to compute the processor numbers of the nearest neighbors in a two-dimensional subset of the hypercube interconnect. If n is the processor number, then half the bits in n represent x location and the other half represent the y location. The x and y node coordinates are converted from gray code to binary, incremented and decremented to obtain coordinates of nearest neighbors, and converted back to gray code to obtain the processor numbers of the four neighbors [17].
A4. [Read problem parameters.] Read the number of timesteps and the subdomain size from the host (step a3).
A5. [Start timesteps.] Initialize the first two timesteps F(i, j) and G(i, j). In the test case, a diagonal shock wave is loaded into the first timestep, and the same wave moved one unit up and to the right is loaded into the second timestep to create a non-dispersing shock; a rectangular region in the path of the wave is marked "reflecting" by setting flags Z(i, j)=0 there. Elsewhere, Z(i, j)=1.
A6. [Main loop.] Transfer the (noncontiguous) left and right "inner edges" of timestep G(i, j) to dedicated contiguous buffers.
A7. [Send boundary messages.] Send all "inner edges" of G to nearest neighbors in the Up, Down, Left, and Right directions. (Boundary conditions are periodic, so processors messages "wrap around" with a toroidal topology).
A8. [Receive boundary messages.] Receive all "outer edges" of G from nearest neighbors in the Down, Up, Right, and Left directions. This interchange of Down-Up, Right-Left provides the maximum possible overlap of communications ( 4.1).
4.1).
A9. [Update timestep.] Use the G timestep to compute a new timestep F using (7), where references to spatial gridpoint neighbors such as F(i+1,j) are replaced by F(i, j) if Z(i+1, j) is 0. Hence, points in the domain that are flagged by Z(i, j) = 0 behave as perfect wave reflectors.
A10. [Send graphics data to host]. If the "History" flag is true, send the pixels representing the wave state to the host for display.
A11. [Update timestep.] Repeat steps A6 to A10, reversing the roles of F and G. This "leapfrog" technique allows the wave to be simulated with only two timesteps in memory at once.
A12. [Next timestep pair.] Repeat steps A6 to A11, for the requested number of timesteps.
A13. [Send last timestep.] Send the pixels representing the final timestep to the host.
A14. [Stop timers.] Record time and send it to the host for performance assessment.
The best known parallel algorithm is computationally identical to the best known serial algorithm; one simply uses a spatial decomposition of the region. Here,  P(N) =
P(N) =  (N), so there is no need to correct for operation efficiency. The sharing of edge data provides all necessary synchronization as timesteps progress. The general approach to the wave equation on a hypercube is described in [8, 17]. We note here a few specifics on the NCUBE version. The program is small enough (about 10 KBytes executable, not including data structures) to load in one long message. By using the full hypercube interconnection (
(N), so there is no need to correct for operation efficiency. The sharing of edge data provides all necessary synchronization as timesteps progress. The general approach to the wave equation on a hypercube is described in [8, 17]. We note here a few specifics on the NCUBE version. The program is small enough (about 10 KBytes executable, not including data structures) to load in one long message. By using the full hypercube interconnection ( 4.5) to load the program, even the full 1024-node jobs load in less than one second.
4.5) to load the program, even the full 1024-node jobs load in less than one second.
5.4.1. Communication cost.
The equations describing communication overhead are
| (8a) | CP(N) = 32N /  P P |
| (8b) | MP(N) = 8 |
where CP(N) is the number of bytes sent and received per timestep per processor, MP(N) is the number of messages sent and received per timestep per processor, N is the number of global gridpoints in the x and y directions, and P is the number of processors (P > 1). For this application, the expressions for communication cost are simple because all messages are to nearest-neighbor processors in the two-dimensional topology. For the smallest problems studied (6 by 6 gridpoints per processor), the communication time per timestep is dominated by the 350 µsec-per-message startup time. The nearest-neighbor communications are described in  4.1 for the largest problems studied (192 by 192 gridpoints per processor). The gather-scatter technique described in
4.1 for the largest problems studied (192 by 192 gridpoints per processor). The gather-scatter technique described in  4.2 is essential in achieving high efficiency for fixed-sized problems.
4.2 is essential in achieving high efficiency for fixed-sized problems.
5.4.2. Computation cost.
In contrast to the other two applications described herein, the wave mechanics problem does relatively few arithmetic calculations per timestep. One consequence of this is that Fortran loop overhead dominates when the subdomains are very small. For example, the 6-by-6 subdomain initially ran at about 40 KFLOPS on a single processor, whereas the 192-by-192 subdomain ran at about 80 KFLOPS on a single processor. Besides degrading absolute performance, this overhead introduced another efficiency loss for the fixed-sized case, since a 50 percent efficiency loss resulting from spatial decomposition had nothing to do with interprocessor communication.
To mitigate this efficiency loss, the kernel of the WAVE timestep update was coded in assembly language. This refinement raised the absolute performance while also flattening performance across the whole range of subdomain sizes. With an assembly version of step A9, the 6-by-6 problem achieved 83 KFLOPS, and larger problems quickly approach a plateau of 111 KFLOPS. Thus a 25 percent loss of efficiency for the fixed-sized case is the result of loop startup time within a single processor, and absolute performance is improved in all cases.
We have used 32-bit precision for this application. The numerical method error is of order (h +  t) [15], which dominates any errors introduced by the finite precision of the arithmetic. The parallel speedup benefits from the larger subdomains permitted by reducing memory requirements from 64-bit words to 32-bit words. Absolute performance is also increased by about 50 percent, with virtually no additional truncation error.
t) [15], which dominates any errors introduced by the finite precision of the arithmetic. The parallel speedup benefits from the larger subdomains permitted by reducing memory requirements from 64-bit words to 32-bit words. Absolute performance is also increased by about 50 percent, with virtually no additional truncation error.
The quadratic equation describing the operation count for each timestep is
| (9) |  P(N) = 9N2 P(N) = 9N2 |
There is no difference between  (N) and
(N) and  1(N). Since there are no terms less than second order, the operation efficiency
1(N). Since there are no terms less than second order, the operation efficiency  P is unity. This ideal value for
P is unity. This ideal value for  P is the main reason that wave mechanics has the highest speedup of the applications presented here.
P is the main reason that wave mechanics has the highest speedup of the applications presented here.
5.5. Measured performance.
By keeping the number of timesteps constant, the resulting performance charts would ideally show constant MFLOPS as a function of problem size, and constant time in seconds as a function of number of processors. It is interesting to compare Tables 1 and 2 against this ideal. Note in particular that time in seconds varies little with hypercube dimension, as one would hope, except for the loss in going from the serial version to the parallel version.
| TABLE 1 |
| MFLOPS for the wave mechanics problem (32-bit arithmetic) |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 192 by 192 | 0.111 | 0.442 | 1.77 | 7.07 | 28.3 | 113 |
| 96 by 96 | 0.111 | 0.442 | 1.77 | 7.06 | 28.2 | 113 |
| 48 by 48 | 0.111 | 0.439 | 1.76 | 7.02 | 28.1 | 112 |
| 24 by 24 | 0.111 | 0.431 | 1.72 | 6.87 | 27.4 | 109 |
| 12 by 12 | 0.106 | 0.400 | 1.59 | 6.32 | 25.0 | 98.1 |
| 6 by 6 | 0.083 | 0.314 | 1.23 | 4.82 | 18.8 | 70.6 |
| TABLE 2 |
| Time in seconds for the wave mechanics problem |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 192 by 192 | 12,780. | 12,806. | 12,809. | 12,817. | 12,822. | 12,824. |
| 96 by 96 | 3,194. | 3,206. | 3,206. | 3,208. | 3,211. | 3,212. |
| 48 by 48 | 796.5 | 805.7 | 805.9 | 806.5 | 807.3 | 808.7 |
| 24 by 24 | 199.3 | 205.5 | 205.8 | 206.1 | 206.6 | 207.8 |
| 12 by 12 | 52.1 | 55.3 | 55.6 | 56.0 | 56.5 | 57.7 |
| 6 by 6 | 16.7 | 17.6 | 18.0 | 18.4 | 19.1 | 20.0 |
The physical problem being solved is identical only along diagonal lines in the above charts, from top left to bottom right. For example, the 12-by-12-per-node problem on a serial processor is the same as a 6-by-6 problem on each of four processors. In contrast, the 192-by-192-per-node problem on an eight-dimensional hypercube is the same as the 96-by-96-per-node problem on a ten-dimensional hypercube; both perform a very high resolution (3072 by 3072 global gridpoints) simulation, but the algorithmic timesteps now represent a smaller interval of physical time for the high-resolution simulation than for the low-resolution simulation, since  t is proportional to 1/N. By fixing the number of algorithmic timesteps, we are able to study the effects of parallel overhead across rows of the table, and the effect of loop overhead along columns.
t is proportional to 1/N. By fixing the number of algorithmic timesteps, we are able to study the effects of parallel overhead across rows of the table, and the effect of loop overhead along columns.
The job with 192 by 192 global gridpoints, the largest problem that spans the entire range of hypercube sizes, yields a fixed-sized speedup of 637. If we scale the problem to fit the processor, always assigning a 192 by 192 subdomain to each node, the overall efficiency never drops below 99.6 percent. In particular, the 1024-node job executes 1020 times as fast as it would on one identical processor with similar access times to 0.5 GByte of memory. Alternatively, the 1024-node job executes at a MFLOPS rate of 1020 times that of a single-node job (see Table 1). Both speedup curves are shown in Fig. 8.
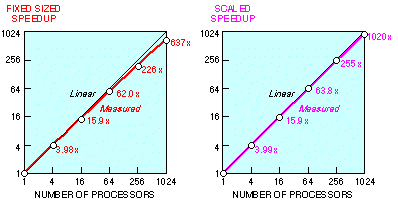
Figure 8. Wave mechanics problem speedups.
This application revealed a series of subtle hardware problems with specific nodes that initially caused a spurious load imbalance of up to 10 percent on the 256-node and 1024-node jobs. By partitioning the cube and comparing times on identical subcubes, we identified "slow nodes" that were performing memory error correction, communication error recovery, or overly frequent memory refresh, all of which diminished performance without causing incorrect results.
The fixed-sized problem speedup of 637 is 62.2 percent of the linear speedup of 1024. Ideally, the fixed-sized 12,780-second serial case would have been reduced to 12.5 seconds; instead, the measured time is 20.0 seconds. Of the 7.5 second difference, 4.2 seconds is due to the reduced MFLOPS rate caused by the shortening of Fortran loop counts on each node (from 192 to 6). This MFLOPS reduction can be observed directly in the leftmost column of Table 1. Another 0.7 seconds is lost in program loading and non-overlapped I/O ( 4.5). The remaining time, 2.6 seconds, is lost in interprocessor communication; the sum of the latter two effects is visible in the bottom row of Table 2. The fixed-sized problem speedup of 637 implies a serial fraction s of 0.0006 (see (1),
4.5). The remaining time, 2.6 seconds, is lost in interprocessor communication; the sum of the latter two effects is visible in the bottom row of Table 2. The fixed-sized problem speedup of 637 implies a serial fraction s of 0.0006 (see (1),  2.1).
2.1).
The scaled problem speedup of 1020 is 99.66 percent of the ideal. Of the 0.34 percent loss, 0 percent is caused by operation efficiency loss ( 5.4.2), 0 percent is lost in loop overhead (since further improvements in serial MFLOPS were negligible beyond the 48-by-48 subdomain size; see Table 1, leftmost column), 0.01 percent is lost in program loading, 0.17 percent is incurred in going from the serial version to the parallel version of the program, and the remaining 0.16 percent is from load imbalance induced by data-dependent MFLOPS rates (
5.4.2), 0 percent is lost in loop overhead (since further improvements in serial MFLOPS were negligible beyond the 48-by-48 subdomain size; see Table 1, leftmost column), 0.01 percent is lost in program loading, 0.17 percent is incurred in going from the serial version to the parallel version of the program, and the remaining 0.16 percent is from load imbalance induced by data-dependent MFLOPS rates ( 3.2). Based on the top row of Table 2, the extrapolated uniprocessor execution time for this problem (6144 by 6144 gridpoints) is approximately 13.1 million seconds (5 months). In the parlance of
3.2). Based on the top row of Table 2, the extrapolated uniprocessor execution time for this problem (6144 by 6144 gridpoints) is approximately 13.1 million seconds (5 months). In the parlance of  2.1, the serial fraction s' is 0.0034, which corresponds to a serial fraction s of approximately 0.000003 (44 seconds of overhead out of 13.1 million seconds).
2.1, the serial fraction s' is 0.0034, which corresponds to a serial fraction s of approximately 0.000003 (44 seconds of overhead out of 13.1 million seconds).
6. Application 2: Fluid dynamics.
6.1. Application description.
The solution of systems of hyperbolic equations often arises in simulations of fluid flow. One technique which has proved successful with hyperbolic fluid problems is Flux-Corrected Transport (FCT) [2, 7]. Such simulations model fluid behavior that is dominated either by large gradients or by strong shocks. The particular application here involves a nonconducting, compressible ideal gas under unstable conditions.
6.2. Mathematical formulation.
FCT is a numerical technique that resolves the solution of the field variables with regions of steep gradients without introducing numerical dispersion or excessive numerical dissipation. Areas of the computational domain that exhibit large flow gradients are resolved using an appropriate weighting of low- and high-order difference schemes so as to preserve positivity of the field variables (for example, density remains positive).
The principles of conservation of mass, momentum and energy for a frictionless, nonconducting compressible gas are represented by the Euler equations. A precise mathematical statement of these laws is expressed in the following set of nonlinear PDE's:
Conservation of Mass:
Conservation of Momentum:
| (11a) | ( u)t + ( u)t + (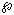 + +  u2)x + ( u2)x + ( uv)y = b(x) uv)y = b(x)
|
| (11b) | ( v)t + ( v)t + ( vu)x + ( vu)x + (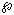 + +  v2)y = b(y) v2)y = b(y)
|
Conservation of Energy:
| (12) | [ (e + u2/2 +v2/2)]t + [ (e + u2/2 +v2/2)]t + [ u(e + u2/2 +v2/2 + u(e + u2/2 +v2/2 + 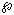 / / )]x )]x
+ [ v(e + u2/2 +v2/2 + v(e + u2/2 +v2/2 + 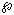 / /  )] y = b(x)u+ b(y)v )] y = b(x)u+ b(y)v
|
where the subscripts denote partial derivatives, b(x) and b(y) represent body force components, u and v are the velocity components in the x and y directions,  is the gas density,
is the gas density, 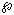 is the gas pressure, and e is the specific internal energy. For simplicity, the computations modeled a thermally perfect ideal gas. The gas law is given by:
is the gas pressure, and e is the specific internal energy. For simplicity, the computations modeled a thermally perfect ideal gas. The gas law is given by:
where 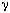 is the constant adiabatic index. (A more complicated equation-of-state would contain more operations and improve the computation/communication ratio).
is the constant adiabatic index. (A more complicated equation-of-state would contain more operations and improve the computation/communication ratio).
6.3. Test problem.
The equations of fluid motion for a frictionless, compressible gas are solved under initial conditions which lead to a well-known Kelvin-Helmholtz instability. The domain is periodic in the x direction, and a shear flow is perturbed in order to produce vortical cells that enlarge with time (Fig. 9). Values Nx and Ny refer to the spatial discretization of the domain for the numerical method described in the next section.
6.4. Parallel Algorithm
ALGORITHM b
Host Program for the Fluid Dynamics Problem
b1. [Start.] Prompt the user for the cube dimension, x and y discretizations (processors and gridpoints), number of timesteps, and the amount of output information.
b2. [Start host timers.] Initialize load timer, read timer, write timer, elapsed timer, and host timer to zero.
b3. [Start nodes.] Open the hypercube with the requested dimension. Load the FCT node program (Algorithm B) into the hypercube using a logarithmic fanout. Send problem parameters to every node using a logarithmic fanout.
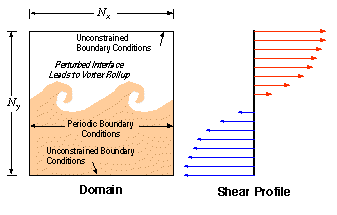
Figure 9. Fluid dynamics problem.
b4. [Assemble processor map.] Compute the mapping of hypercube nodes to the two-dimensional domain (cf. step A3,  5.4) for the purpose of sorting output from hypercube nodes. (This overlaps the node computation of the first timestep.)
5.4) for the purpose of sorting output from hypercube nodes. (This overlaps the node computation of the first timestep.)
b5. [Read timestep.] If the timestep was one requested as output, read the information from the hypercube nodes.
b6. [Iterate.] Repeat step b5 for every timestep.
b7. [Read node timers.] Read the node timing information after cessation of hypercube calculations.
b8. [Close hypercube.] Close the allocated array in the physical hypercube.
b9. [Stop host timers.] Stop all timers initialized in step b2.
b10. [Display timers and stop.] Write out all host and node times to requested output devices.
ALGORITHM B
Node Program for the Fluid Dynamics Problem
B1. [Start timers.] Initialize all node performance timers.
B2. [Problem setup] Read input values (step b3) and generate initial values for  ,
,  u,
u,  v, and e.
v, and e.
B3. [Calculate extensive variables.] Compute the latest values of  , u, and v for the current time based on the values of
, u, and v for the current time based on the values of  ,
,  u,
u,  v, and e.
v, and e.
B4. [Calculate  t] Calculate new timestep based on current values of the dependent variables, using a global exchange (
t] Calculate new timestep based on current values of the dependent variables, using a global exchange ( 4.4).
4.4).
B5. [Communicate dependent variables.] Communicate with four neighbors the edge values for all dependent variables:  ,
, u,
u, v, and e.
v, and e.
B6. [Communicate extensive variables.] Communicate with four neighbors the edge values of all extensive variables:  , u, and v.
, u, and v.
B7. [Advance density by  t/2.] Calculate
t/2.] Calculate  and exchange two-deep edges with the four neighbors.
and exchange two-deep edges with the four neighbors.
B8. [Advance x momentum component by  t/2.] Calculate
t/2.] Calculate  u and exchange two-deep edges with the four neighbors.
u and exchange two-deep edges with the four neighbors.
B9. [Advance y momentum component by  t/2.] Calculate
t/2.] Calculate  v and exchange two-deep edges with the four neighbors.
v and exchange two-deep edges with the four neighbors.
B10. [Advance specific internal energy by  t/2.] Calculate e and exchange two-deep edges with the four neighbors.
t/2.] Calculate e and exchange two-deep edges with the four neighbors.
B11. [Use half-timestep values to finish timestep.] Repeat steps B3 to B10 to advance all dependent variables from current time to current time plus  t.
t.
B12. [Send data to host.] Send graphical and tabular data to output devices as requested.
B13. [Next timestep.] Repeat steps B3 to B12 for the requested number of timesteps.
B14. [Record the times.] Stop all timers; send times to the host, and quit.
There are several features of FCT which make it especially suitable for large-scale parallel processors. First, the number of operations performed at each grid cell is independent of the data. Thus, processor load balance is not affected by regions with high activity, such as shocks, since the same computations are performed in the regions with low activity, or low fluid gradients. Even though these problems are nonlinear, there are no data-dependent computational decisions (branches) made during the simulations.
Second, the calculations are performed over a fixed mesh. This feature allows us to always optimally decompose the computational grid statically, perfecting the load balance and minimizing communication costs.
Third, the nonlinear partial differential equations are solved explicitly, meaning that only data from the previous time level is needed to advance the solution to the next time step. Only a single global communication is needed per timestep in order to advance the time based on CFL condition limitations.
6.4.1. Communication cost.
All of the interprocessor communications associated with the grid decomposition are nearest-neighbor only. One global communication occurs each timestep in step B4, when all processors must determine the shortest possible transit time across any cell for which they are responsible, and broadcast that time to all processors to determine the maximum allowable timestep (CFL condition). The exchange is accomplished via nearest- neighbor data exchanges along each dimension of the hypercube ( 4.4); thus, this global communication is performed in only log2P time.
4.4); thus, this global communication is performed in only log2P time.
The equations describing communication overhead are
| (14a) | CP(nx, ny) = 1472(nx + ny) + 48 log2P |
| (14b) | MP(nx, ny) = 96 + 2 log2P |
where nx and ny are the number of gridpoints per processor in the x and y directions. The log2P terms in (14a) and (14b) are the result of the global exchange used to calculate the maximum timestep permitted by the CFL condition (step B4). The other terms are the result of nearest-neighbor communications ( 4.1), which exchange one or two strips of data between adjacent processors in all four directions on the grid.
Fig. 10 shows measurements for the nearest-neighbor communication times of steps B7 through B10. Measurements for the remaining nearest-neighbor communications in steps B5 and B6 show a similar slope and intercept. Attempts to use (14a) and (14b) to predict nearest-neighbor communication times, using the measured parameters of Fig. 10 (startup time and time per byte), predict times twice as large as measured. This discrepancy is indicative of communication overlap which would not be accounted for by the substitution of parameters into (14a) and (14b), as explained in
4.1), which exchange one or two strips of data between adjacent processors in all four directions on the grid.
Fig. 10 shows measurements for the nearest-neighbor communication times of steps B7 through B10. Measurements for the remaining nearest-neighbor communications in steps B5 and B6 show a similar slope and intercept. Attempts to use (14a) and (14b) to predict nearest-neighbor communication times, using the measured parameters of Fig. 10 (startup time and time per byte), predict times twice as large as measured. This discrepancy is indicative of communication overlap which would not be accounted for by the substitution of parameters into (14a) and (14b), as explained in  4.1.
4.1.
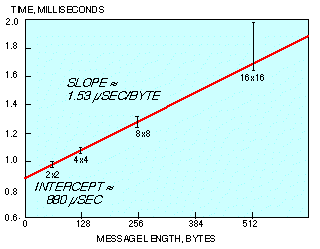
Figure 10. Nearest-neighbor communication-pair times.
| TABLE 3 |
Operation efficiency 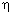 P for the fluid dynamics problem P for the fluid dynamics problem |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 64 by 64 | 1.0000 | 0.9975 | 0.9963 | 0.9957 | 0.9953 | 0.9952 |
| 32 by 32 | 1.0000 | 0.9950 | 0.9926 | 0.9913 | 0.9907 | 0.9904 |
| 16 by 16 | 1.0000 | 0.9903 | 0.9853 | 0.9829 | 0.9817 | 0.9810 |
| 8 by 8 | 1.0000 | 0.9801 | 0.9706 | 0.9657 | 0.9632 | 0.9619 |
| 4 by 4 | 1.0000 | 0.9610 | 0.9416 | 0.9323 | 0.9274 | 0.9248 |
| 2 by 2 | 1.0000 | 0.9236 | 0.8869 | 0.8684 | 0.8590 | 0.8538 |
6.4.2. Computation cost. The equation describing the total operation count for each timestep is:
| (15) |  P(Nx, Ny ) = 54P + 3Plog2P + 20Nx P(Nx, Ny ) = 54P + 3Plog2P + 20Nx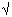 P + 348Ny P + 348Ny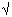 P + 1158 NxNy P + 1158 NxNy
|
The serial operation count is the same as the parallel operation count for one processor; i.e.,  (Nx, Ny ) =
(Nx, Ny ) =  1(Nx, Ny ).
1(Nx, Ny ).
The low-order terms in (15) cause operational efficiency 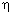 P to be less than unity. The largest part of the operational efficiency loss is caused by the 348Ny
P to be less than unity. The largest part of the operational efficiency loss is caused by the 348Ny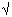 P term, which results from the transfer of calculations from inner loops to outer loops. This movement of computation from the square term (inner loop) to the linear term (outer loop) reduces the total amount of work, improving the serial processor time. The effect decreases with increasing problem size. Alternatively, by moving the computation into the inner loop we would degrade serial performance slightly but increase net speedup. When the number of processors is large, subtle programming changes can cause large fluctuations in fixed-sized problem speedup.
P term, which results from the transfer of calculations from inner loops to outer loops. This movement of computation from the square term (inner loop) to the linear term (outer loop) reduces the total amount of work, improving the serial processor time. The effect decreases with increasing problem size. Alternatively, by moving the computation into the inner loop we would degrade serial performance slightly but increase net speedup. When the number of processors is large, subtle programming changes can cause large fluctuations in fixed-sized problem speedup.
Table 3 shows the operation efficiency for the range of problem sizes studied in the next section. These efficiencies are incorporated into the measured performance. Note that the operation efficiency loss is as large as 15 percent.
6.5. Measured performance. The results are shown in Table 4 and Table 5 for 1600-timestep jobs. The fixed-sized problem uses a 64-by-64 grid, with 2-by-2 points per processor for the 1024-node case.
The fixed-sized and scaled speedup curves for the FCT program are shown in Fig. 11. The fixed-sized speedup of 519 is 50.7 percent of the ideal linear speedup of 1024. A perfect speedup would have yielded an execution time of 108 seconds, rather than the measured 214 seconds. This 106-second discrepancy is the result of four major sources
| TABLE 4 |
| MFLOPS for the fluid dynamics problem (64-bit arithmetic) |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 64 by 64 | 0.0687 | 0.274 | 1.09 | 4.35 | 17.4 | 69.3 |
| 32 by 32 | 0.0683 | 0.272 | 1.08 | 4.33 | 17.2 | 68.8 |
| 16 by 16 | 0.0676 | 0.267 | 1.06 | 4.23 | 16.9 | 67.5 |
| 8 by 8 | 0.0663 | 0.255 | 1.01 | 4.02 | 16.0 | 63.7 |
| 4 by 4 | 0.0648 | 0.230 | 0.888 | 3.50 | 13.8 | 55.0 |
| 2 by 2 | 0.0594 | 0.167 | 0.596 | 2.30 | 9.04 | 35.6 |
| TABLE 5 |
| Time in seconds for the fluid dynamics problem |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 64 by 64 | 111,098 | 111,149 | 111,433 | 111,776 | 111,913 | 112,221 |
| 32 by 32 | 28,039 | 28,059 | 28,068 | 28,099 | 28,179 | 28,258 |
| 16 by 16 | 7,159 | 7,174 | 7,180 | 7,187 | 7,195 | 7,204 |
| 8 by 8 | 1,861 | 1,894 | 1,893 | 1,898 | 1,904 | 1,909 |
| 4 by 4 | 495 | 536 | 545 | 547 | 551 | 553 |
| 2 by 2 | 144 | 192 | 207 | 210 | 212 | 214 |
of inefficiency: uniprocessor loop overhead is 17 seconds, as derived from the leftmost column of Table 3. Communication overhead in the parallel version is 66 seconds as measured by the node timers. Operation inefficiency accounts for 21 seconds, or 14.6 percent (cf. Table 4). Program loading, and non-overlapped I/O, which require about 2 seconds, are the remaining sources of inefficiency. The fixed-sized problem speedup of 519 implies a serial fraction s of 0.001 (see (1),  2.1).
2.1).
The scaled speedup of 1009 is 98.5 percent of the ideal. In this case, the operation efficiency is 99.5 percent. Communication overhead, program loading, and startup account for the remaining 1.0 percent loss in efficiency. Based on the top row of Table 5, the extrapolated uniprocessor execution time for this 2048-by-2048-gridpoint problem is approximately 114 million seconds (3.6 years). In the parlance of  2.1, the serial fraction s' is 0.013, which corresponds to a serial fraction s of approximately 0.00001 (1120 seconds of overhead out of 114 million seconds).
2.1, the serial fraction s' is 0.013, which corresponds to a serial fraction s of approximately 0.00001 (1120 seconds of overhead out of 114 million seconds).
7. Application 3: Beam-strain analysis.
7.1. Application description. Finite element techniques are used, for example, in structural analysis, fluid mechanics, and heat transfer applications. The particular application selected here involves the deflection of a beam subject to a specified load. This application is an established benchmark in structural mechanics, because the resulting matrix equations tend to be poorly conditioned, which mandates the use of high-precision arithmetic and a large number of iterations to achieve convergence with standard iterative solution methods.
Figure 11. Fluid dynamics problem speedups.
7.2. Mathematical formulation. The differential equations of equilibrium in plane elasticity, which are used in the BEAM program, are presented in [21] with their finite element formulation. The equations can be summarized as
| (16a) | auxx + bvxy + G(uyy + vxy ) + Fx = 0 |
| (16b) | buxy + avyy + G(uxy + vxx ) + Fy = 0 |
where the subscripts denote partial derivatives, u and v represent displacement components in the x and y directions respectively, Fx and Fy are force components, and a, b, and G are constitutive equation parameters. The latter can, in turn, be expressed in terms of the moduli of elasticity and rigidity, and Poisson's Ratio.
The preferred methods at Sandia for solving structural analysis problems are finite elements to approximate the physical/mathematical model and Preconditioned Conjugate Gradients (PCG) to solve the resulting large, sparse set of linear equations, Ax = b. These methods are used in the solid mechanics application program JAC [6], a highly-vectorized serial production program used on the CRAY X-MP, as well as the new, highly parallel BEAM program. Jacobi (main diagonal) preconditioning is used in both programs because it vectorizes and can be made parallel. 64-bit precision is used throughout the program; convergence is difficult without it.
The parallel BEAM program never forms and stores the stiffness matrix A in memory and hence is able to solve systems of equations several times larger than if the matrix were formed explicitly. The only place that the stiffness matrix appears in the standard PCG algorithm [11] is in the matrix-vector product with the projection vector p. If residual and iterate vectors are denoted as b and x, respectively, then approximation of the matrix-vector product by a difference formula for the directional derivative can be expressed as
| (17) | Apk = (b(x0 +  pk) - b(x0)) / pk) - b(x0)) /  |
where k is the iteration counter and e is the difference parameter. The matrix-free procedure given by (17) saves storage of A and repeated calculation of matrix-vector products, at the price of an additional residual vector calculation at each iteration.
7.3. Test problem. As shown in Fig. 12, the BEAM program computes the deflection of a two-dimensional beam fixed at one end, subject to a specified force, F. The beam is modeled as a linearly elastic structure with a choice of plane-strain or plane-stress constitutive equations. Values Nx and Ny refer to the spatial decomposition for the numerical method described in  7.4.2.
7.4.2.
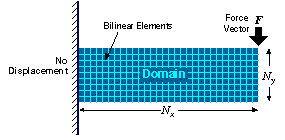
Figure 12. Beam-strain analysis problem.
7.4. Parallel implementation.
ALGORITHM c
Host Program for the Beam-Strain Analysis Problem
c1. Prompt the user for input values. (Read the dimension of the cube, number of processors and finite elements in the x and y directions, and physical parameters of the beam model).
c2. Open a hypercube, and send a copy of the program (Algorithm C) to all nodes using a logarithmic fanout. (Nodes begin execution, and start timing their job, as soon as they are loaded.)
c3. Send the input values to node 0 (step C3).
c4. While the first iteration is being calculated, create the output header.
c5. Print the input values from step c1 to the output file.
c6. Collect output data from node 0 and print them in the output file. (All nodes contain copies of data resulting from global exchanges; therefore, only one node needs to send the final result to the host.) The message type indicates completion of iterations, continuation of iterations, or any of a number of failure modes.
c7. If message type indicates continuation of iterations, then repeat step c6.
c8. Close the hypercube.
ALGORITHM C
Node Program for the Beam-Strain Analysis Problem
C1. [Start timer.] Record the time.
C2. [Get node ID.] Execute a system call to obtain this node's processor number (0 to 1023, gray code) and the dimension of the cube.
C3. [Get job parameters.] If the processor number is 0, receive job parameters from the host (step c3). (This data is then propagated using the logarithmic fanout shown in  4.5.)
4.5.)
C4. [Create two-dimensional topology.] Use the data from C2 and C3 to compute the processor numbers of the nearest neighbors in a two-dimensional subset of the hypercube interconnect. (This is done as described for the Wave Mechanics problem, except that Nx is not necessarily equal to Ny.)
C5. [Decompose domain.] Based on the position in the two-dimensional global domain, compute the finite element basis functions, mesh points, initial iteration guess, x0, boundary conditions, and relationships between mesh points and elements.
C6. [Start nonlinear iteration.] Set up Newton iteration: calculate residual vector b by 2-by-2-point Gaussian quadrature and save a copy of it as b0.
C7. [Start linear iteration.] Set up PCG iteration: calculate and invert d, the main diagonal of the iteration matrix A. Initialize projection vector p and vector Ap to zero. Start iteration loop timer.
C8. [Start iteration loop.] Set iteration counter i to 1.
C9. [Precondition b.] Calculate z = dIb, where I is the identity matrix. Exchange boundary values of z.
C10. [Find directional derivative.] Compute "matrix-free" product Az using b(x0 +  z). Compute b(x0 +
z). Compute b(x0 +  z), then exchange and sum boundary values. Compute Az (see (17).)
z), then exchange and sum boundary values. Compute Az (see (17).)
C11. [Prepare z for inner product calculation.] Reset "left" and "up" boundary values of z to zero.
C12. [Compute inner products.] Calculate local portion of z b, z
b, z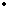 Az, and p
Az, and p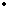 Az. Perform a global exchange (
Az. Perform a global exchange ( 4.4) to obtain global inner products.
4.4) to obtain global inner products.
C13. [Test for convergence.] If z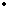 b <
b <  , then stop iteration loop timer and proceed with step C15. If iteration number i is a multiple of input parameter j and node number is 0, send inner products to host for monitoring progress of calculation.
, then stop iteration loop timer and proceed with step C15. If iteration number i is a multiple of input parameter j and node number is 0, send inner products to host for monitoring progress of calculation.
C14. [Calculate projection length 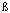 ].
]. 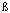 is z
is z b divided by the value of z
b divided by the value of z b from the previous iteration. Then Ap = Az +
b from the previous iteration. Then Ap = Az + 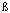
 Ap and p
Ap and p Ap = z
Ap = z Az + 2
Az + 2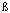 p
p Az +
Az + 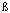 2p
2p Ap.
Ap.
C15. [Update linear solution.] Calculate  in the PCG algorithm (
in the PCG algorithm ( = z
= z b/ p
b/ p Ap ) and update p, x, and b. (p = z +
Ap ) and update p, x, and b. (p = z + 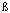 p, x = x +
p, x = x + 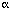 p, b = b -
p, b = b - 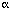 Ap). Increase i by 1 and go to step C9 if i is less than or equal to the maximum number of iterations (specified as a job parameter). If i exceeds that maximum, stop the iteration loop timer, send a message to the host that linear iteration failed and proceed to step C17.
Ap). Increase i by 1 and go to step C9 if i is less than or equal to the maximum number of iterations (specified as a job parameter). If i exceeds that maximum, stop the iteration loop timer, send a message to the host that linear iteration failed and proceed to step C17.
C16. [Update the nonlinear solution.] If the problem is linear or the Newton iteration has converged, send a message indicating this to the host. If the maximum number of nonlinear iterations has exceed the maximum (specified as a job parameter), send a message indicating this to the host. Otherwise, calculate a new residual vector b by Gaussian quadrature and go to step C7.
C17. [Complete node timings.] Gather overall and step C6-C16 timing statistics by a global exchange. Stop node timer. Send complete timing statistics to the host (step c6).)
The parallel formulation of the PCG and finite element algorithms used in BEAM is based on spatial decomposition. Each processor is assigned a rectangular subdomain within the computational domain of the beam. Each processor subdomain can, in turn, contain thousands of finite elements. The necessary synchronizations during each conjugate gradient iteration are provided by three communication steps:
- Exchange subdomain edge values of the preconditioned residual vector ,z (step C9) with the four processors which are nearest neighbors on both the hypercube and the gray-coded computational domain. Send boundary values of z to the nearest neighbor "down", and receive boundary values of z from the nearest neighbor "up" in the gray code decomposition. Send boundary values of z to the nearest neighbor "right", and receive boundary values of z from the nearest neighbor "left" in the gray code decomposition. This explicit sharing of data allows the matrix-vector partial product to be done locally without any further communication.
- Exchange and add subdomain edge values of the perturbed residual vector b(x0 +
 z) (step C10) with the four processors which are nearest neighbors on both the hypercube and the gray-coded computational domain. Send boundary values of b(x0 +
z) (step C10) with the four processors which are nearest neighbors on both the hypercube and the gray-coded computational domain. Send boundary values of b(x0 +  z) to the nearest neighbor "left," receive boundary values of b(x0 +
z) to the nearest neighbor "left," receive boundary values of b(x0 +  z) from the nearest neighbor "right," and add to the b(x0 +
z) from the nearest neighbor "right," and add to the b(x0 +  z) boundary. Send boundary values of z to the nearest neighbor "up," and receive boundary values of z from the nearest neighbor "down," and add to the b(x0 +
z) boundary. Send boundary values of z to the nearest neighbor "up," and receive boundary values of z from the nearest neighbor "down," and add to the b(x0 +  z) boundary.
z) boundary.
- Perform global exchange and accumulation of three data items (
 4.4): inner products z
4.4): inner products z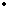 b, z
b, z Az, and p
Az, and p Az used in PCG iteration and convergence test (step C11).
Az used in PCG iteration and convergence test (step C11).
Parallel PCG algorithms have been previously reported for the CRAY X-MP [19] and ELXSI 6400 [16]. Another investigation [3] recognized that the algorithm can be restructured to reduce memory and communication traffic, as well as synchronization. We find that, by precalculating the quantity Az in place of Ap in the PCG iteration loop (step C10), the calculation of some inner products can be postponed to make possible the calculation of all inner products in an iteration in one global exchange. The potential reduction in communication time due to fewer global exchanges is 50 percent; reductions of about 25 percent are observed for small, communication-dominated problems, e.g., a total of 2048 bilinear elements on 1024 processors. The new algorithm does not increase computation time (and, therefore, serial execution time of our best serial algorithm), but does require storage of an additional vector to hold precalculated information.
7.4.1. Communication cost. The communication cost per iteration step for the BEAM program is given by
| (18a) | CP(nx, ny) = 64 (nx + ny) + 48 log2P |
| (18b) | MP (nx, ny) = 8 +2 log2P |
where these equations, like those of  5.4.1 and
5.4.1 and  6.4.1, do not account for possible overlap of messages. The log2P terms result from a global exchange used to calculate global inner products (step C12). The remaining terms arise from nearest neighbor communications (steps C9 and C10).
6.4.1, do not account for possible overlap of messages. The log2P terms result from a global exchange used to calculate global inner products (step C12). The remaining terms arise from nearest neighbor communications (steps C9 and C10).
7.4.2. Computation cost. As shown in Table 6, rates of 132 MFLOPS are observed. The essential operation count in each pass through the iteration loop is
| (19) |  (Nx, Ny) = 111 + 80 (Nx + Ny ) + 930 Nx Ny (Nx, Ny) = 111 + 80 (Nx + Ny ) + 930 Nx Ny |
where Nx and Ny are the number of finite elements (rather than gridpoints) in the x and y directions, respectively. The actual number of operations performed in the parallel version differs from (19). To save communication, a few operations are performed redundantly on all processors so that the parallel operation count is given by
| (20) |  P(Nx, Ny ) = 115P + 5Plog2P + 82(Nx + Ny) P(Nx, Ny ) = 115P + 5Plog2P + 82(Nx + Ny) P + 930NxNy P + 930NxNy |
where P is the number of processors. (Note that unlike the previous two applications,  (Nx, Ny)
(Nx, Ny) 
 1(Nx, Ny). This inequality is a consequence of exchange and addition of boundary values in step C10.) Hence,
1(Nx, Ny). This inequality is a consequence of exchange and addition of boundary values in step C10.) Hence, 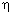 P is a major source of parallel overhead. The operation efficiency
P is a major source of parallel overhead. The operation efficiency  P is shown in Table 6.
P is shown in Table 6.
7.5 Measured performance. The largest problem that fits on the full range of hypercube dimensions is the 2048 bilinear finite element discretization. This problem barely fits in one node, requiring all but a few KBytes of the 512 KByte total node storage. On 1024 processors, the memory required is only that which is necessary for two
| TABLE 6 |
Operation efficiency  P for the beam-strain analysis problem P for the beam-strain analysis problem |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 64 by 32 | 1.0000 | 0.9978 | 0.9968 | 0.9963 | 0.9961 | 0.9960 |
| 32 by 16 | 1.0000 | 0.9956 | 0.9936 | 0.9926 | 0.9921 | 0.9918 |
| 16 by 8 | 1.0000 | 0.9910 | 0.9868 | 0.9848 | 0.9838 | 0.9833 |
| 8 by 4 | 1.0000 | 0.9808 | 0.9723 | 0.9683 | 0.9663 | 0.9654 |
| 4 by 2 | 1.0000 | 0.9578 | 0.9403 | 0.9322 | 0.9284 | 0.9264 |
| 2 by 1 | 1.0000 | 0.9040 | 0.8676 | 0.8518 | 0.8444 | 0.8409 |
| TABLE 7 |
| MFLOPS for the beam strain-analysis problem (64-bit arithmetic) |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 64 by 32 | 0.130 | 0.517 | 2.07 | 8.26 | 33.0 | 132. |
| 32 by 16 | 0.129 | 0.512 | 2.04 | 8.16 | 32.6 | 130. |
| 16 by 8 | 0.129 | 0.507 | 2.01 | 8.02 | 32.0 | 128. |
| 8 by 4 | 0.129 | 0.495 | 1.94 | 7.69 | 30.5 | 121. |
| 4 by 2 | 0.130 | 0.461 | 1.75 | 6.78 | 26.4 | 103. |
| 2 by 1 | 0.130 | 0.375 | 1.30 | 4.77 | 17.8 | 67.1 |
bilinear elements (about 400 bytes) plus Gaussian quadrature constants, global inner products, projection and residual vectors of the PCG iteration, and the program itself. Measurements are shown in Tables 7 and 8.
Job times are compared per 100 iterations for this application to allow the same kind of comparative analysis as in the previous applications: loop overhead by columns and parallel overhead by rows. The number of iterations required to converge increases approximately as Nx and Ny. All of these calculations were run to convergence, with one exception: the calculation in the upper right corner of Tables 7 and 8. This job, with a 2048-by-1024 grid of finite elements on the full hypercube, requires more than one week to reach the converged solution. Time spent outside the iteration loop has been averaged into the results of Table 8.
The problem execution time drops slightly when the largest problem size is run on four processors rather than serially (Table 8, columns 1 and 2). Partitioning the problem among processors gives each processor residual equations of similar magnitude, which results in reduced floating-point normalization ( 3.2) for all problem sizes. On the largest problem size, this effect more than compensates for the addition of interprocessor communication time for the four processor case relative to the serial case. This result implies that a more computationally efficient ordering of equations for the single processor case is possible (but not necessarily practical).
3.2) for all problem sizes. On the largest problem size, this effect more than compensates for the addition of interprocessor communication time for the four processor case relative to the serial case. This result implies that a more computationally efficient ordering of equations for the single processor case is possible (but not necessarily practical).
The problem size is constant along the diagonals in the Tables, from top left to lower right. For example, the 64-by-32 grid of finite elements per node problem on a serial processor is the same as the 32-by-16 grid of finite elements per node problem on each of four processors. The case of a problem with a 64-by-32 grid of finite elements spans the entire range of hypercube sizes. The problem was run to convergence for better measurement of fixed-sized speedup. The elapsed time, MFLOPS rate, number of iterations required for convergence, and fixed-sized speedup are indicated in Table 9.
| TABLE 8 |
| Time in seconds per 100 iterations for the beam-strain analysis problem. |
| | | | Hypercube dimension | | |
| Problem size per node | 0 | 2 | 4 | 6 | 8 | 10 |
| 64 by 32 | 1499.8 | 1499.6 | 1500.2 | 1500.8 | 1501.1 | 1501.7 |
| 32 by 16 | 378.4 | 379.3 | 379.9 | 380.4 | 380.9 | 381.3 |
| 16 by 8 | 95.5 | 96.4 | 97.0 | 97.5 | 97.9 | 98.4 |
| 8 by 4 | 24.3 | 25.1 | 25.6 | 26.1 | 26.5 | 27.0 |
| 4 by 2 | 6.30 | 7.07 | 7.58 | 8.02 | 8.45 | 8.88 |
| 2 by 1 | 1.73 | 2.46 | 2.97 | 3.40 | 3.84 | 4.27 |
| Result extrapolated from 30 iterations |
| TABLE 9 |
| Beam-strain analysis fixed-sized problem (2048 elements) |
| Hypercube Dimension | Job Time, seconds | Speed, MFLOPS | Number of Iterations | Fixed speedup |
| 0 | 16,278. | 0.128 | 1,087 | 1.00 |
| 2 | 4,097.6 | 0.508 | 1,088 | 3.97 |
| 4 | 1,038.8 | 2.00 | 1,087 | 15.7 |
| 6 | 272.25 | 7.67 | 1,087 | 59.8 |
| 8 | 80.01 | 26.4 | 1,087 | 203. |
| 10 | 32.44 | 67.1 | 1,088 | 502. |
If we scale the problem to fit the processor, with a 64-by-32 element subdomain on each node, the efficiency never drops below 99.5 percent. In particular, the 1024 processor job executes 1019 times as fast as a single processor would if it had access to 0.5 GBytes of memory. This scaled speedup result is given by the right graph of Fig. 13.
The fixed-sized speedup of 502 is 49.0 percent of the ideal linear speedup. Perfect speedup would have yielded execution time of 15.9 seconds, rather than the measured 32.4 seconds. The discrepancy is the result of three sources of inefficiency: Communication overhead in the parallel version is 10.9 seconds of the total 32.4 seconds reported in Table 9. Operation inefficiency is 3.4 seconds, or 15.9 percent (cf. Table 6) of the 21.5 seconds of computation. Program loading and startup, which require about 2 seconds ( 2.3.1), are the remaining sources of inefficiency. Unlike the two previous applications, uniprocessor loop overhead is negligible, as shown by the leftmost column of Table 7. The MFLOPS rate changes little because most of the compute-intensive inner loops are Gaussian quadratures with loop counts that are independent of nx and ny. The fixed-sized problem speedup of 502 implies a serial fraction s of 0.001 (see (1),
2.3.1), are the remaining sources of inefficiency. Unlike the two previous applications, uniprocessor loop overhead is negligible, as shown by the leftmost column of Table 7. The MFLOPS rate changes little because most of the compute-intensive inner loops are Gaussian quadratures with loop counts that are independent of nx and ny. The fixed-sized problem speedup of 502 implies a serial fraction s of 0.001 (see (1),  2.1).
2.1).
The scaled speedup of 1019 is 99.5 percent of the ideal. In this case, the operation efficiency is 99.6 percent. Communication overhead, program loading, and startup account for the remaining 0.1 percent loss in efficiency. When taken to convergence, the accrued overhead (including operation efficiency loss) is about 3000 seconds. The extrapolated uniprocessor execution time for this problem (two million finite elements) is
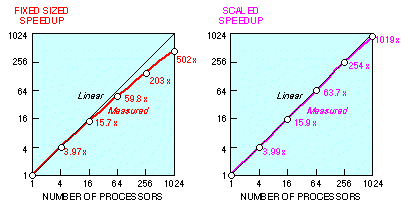
Figure. 13. Beam-strain analysis problem speedups.
approximately 20 years. In the parlance of  2.1, the serial fraction s' is 0.005, which corresponds to a serial fraction s of approximately 0.000005 (3000 seconds of overhead out of 600 million seconds).
2.1, the serial fraction s' is 0.005, which corresponds to a serial fraction s of approximately 0.000005 (3000 seconds of overhead out of 600 million seconds).
8. Summary and discussion. For three important scientific applications-wave mechanics, fluid dynamics, and beam strain analysis-we have developed massively parallel solution programs. Moreover, the algorithms appear extensible to higher levels of parallelism than the 1024-processor level validated in this paper. We have examined the relationship between Amdahl's fixed-sized paradigm and a scaled paradigm to assess parallel performance. The scaled paradigm allows one to evaluate ensemble performance over a much broader range of problem sizes and operating conditions than does the fixed-sized paradigm. For the fixed-sized problems, efficiencies range between 0.49 to 0.62. For the scaled problems, efficiencies range between 0.987 to 0.996. The performance for the three applications, for both fixed-sized problems and scaled problems, is summarized in Table 10.
Because the applications presented here achieve parallel behavior close to ideal, subtle effects appear in the efficiency that have been relatively unimportant in the past. The body of literature showing parallel speedup indicates that communication cost, algorithmic load imbalance, and serial parts of algorithms have accounted for virtually all efficiency loss in parallel programs. We have reduced those effects to the point where new ones become prominent. These new effects are potential hindrances to parallelism on larger ensembles.
The serial fraction s ranged from 0.0006 to 0.001 for the fixed-sized problems. This is smaller than one might generally associate with a real application. However, s decreases with problem size. When the problem size is scaled with the number of processors, the serial fraction s' is 0.003 to 0.013, corresponding to an equivalent serial fraction s of 0.000003 to 0.00001. This validates the scaled problem model of  2.1.
2.1.
Operation efficiency, an algorithmic consideration, is the dominant term in accounting for the efficiency loss in scaled speedup measurements for two of the three applications. The factoring of efficiency into two components, processor usage efficiency and performed/required operation efficiency, appears to be new to the literature. Operation efficiency is an important new tool for analysis and development of highly parallel algorithms. It can be used to tune parallel performance by providing an analytical model of the tradeoff between communication overhead and redundant operations.
Subtle efficiency losses can also be caused by the hardware of massively parallel ensembles. First, data-dependent timing for basic arithmetic is responsible for much of the load imbalance in the scaled applications. Even though each processor performs a
| TABLE 10 |
| Performance summary for applications studied. |
| | 1024-processor speedup | 1024-processor MFLOPS |
| Application | Scaled | Fixed-sized | Scaled | Fixed-sized |
Baffled surface wave simulation
using finite differences | 1,020 | 637 | 113 | 71 |
Unstable fluid flow
using flux-corrected transport | 1,009 | 519 | 69 | 36 |
Beam strain analysis
using conjugate gradients | 1,019 | 502 | 132 | 67 |
nearly identical set of arithmetic operations (except at boundary conditions), a measured statistical skew is caused by the variation in time required for floating-point operations on the current VLSI node processor. The effect is less than 1 percent in all cases, but becomes visible on applications such as wave mechanics where the algorithmic load balance is perfect.
Second, in measuring the performance on various sized subcubes, anomalies were observed. These anomalies could be reproduced, for example, on the lowest 512 processors but not the upper 512 processors. An almost-perfect efficiency was reduced to 90 to 97 percent efficiency when the subcube in use contained certain defective processor nodes. Close examination of the nodes revealed various defects that slowed their operation without causing incorrect results: communication errors with successful retries, error corrections on memory, and hyperactive dynamic RAM refresh rates. The three applications served, and continue to serve, as "slow node" diagnostics for finding and replacing defective nodes. It is unlikely that they could have served this purpose had they not been nearly 100 percent efficient. The statistical base of processors is large enough that anomalies in hardware performance are readily apparent; this effect will become increasingly important as processor ensembles increase in size.
It is important to note that, even when we are constrained to a fixed-sized problem, the ensemble MFLOPS rate is equivalent to the vector MFLOPS rate of typical supercomputers. When mesh sizes are scaled up to those typical of the large PDE simulations used in scientific and engineering analysis, the result is nearly perfect (linear) speedup. This work is strong evidence of the power and future of parallel computing with large numbers of processors.
Acknowledgements. We thank Melvin Baer for discussions regarding FCT algorithms and applications and John Biffle for discussions on the bending beam and related solid mechanics applications. We appreciate suggestions concerning this paper that were provided by colleagues at Sandia, including Edwin Barsis, George Davidson, Gerald Grafe, Victor Holmes, Steven Humphries, Guylaine Pollock, and Gilbert Weigand. We acknowledge the staff of NCUBE Corporation for their support. Finally, we thank Gordon Bell and Alan Karp for the stimulus that their challenges have provided to our work, and to the scientific computing community as a whole.
REFERENCES
- G. AMDAHL, Validity of the single-processor approach to achieving large-scale computer capabilities, AFIPS Conference Proceedings 30, (1967), pp. 483-485.
- M. R. BAER AND R. J. GROSS, A two-dimensional flux-corrected transport solver for convectively dominated flows, Sandia Report SAND85-0613, Sandia National Laboratories, Albuquerque, NM, 1986.
- D. BARKAI, K. J. M. MORIARTY, AND C. REBBI, A modified conjugate gradient solver for very large systems, Proceedings of the 1985 International Conference on Parallel Processing, (1985), pp. 284-290.
- E. BARSIS, Private communication, Sandia National Laboratories, 1987.
- R. E. BENNER, J. L. GUSTAFSON, AND G. R. MONTRY, Analysis of scientific application programs on a 1024-processor hypercube, Report for the 1988 Gordon Bell Competition, Sandia National Laboratories, Albuquerque, NM, 1987.
- J. H. BIFFLE, JAC-A two-dimensional finite element computer program for the non-linear quasistatic response of solids with the conjugate gradient method, Report SAND81-0998, Sandia National Laboratories, Albuquerque, NM, 1984.
- J. P. BORIS AND D. L. BOOK, Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works, Journal of Computational Physics, 18, (1973), pp. 38-69.
- R. CLAYTON, Finite difference solutions of the acoustic wave equation on a concurrent processor, Caltech publication HM-89, California Institute of Technology, Pasadena, 1985.
- G. C. FOX AND S. W. OTTO, Algorithms for concurrent processors, Physics Today, 37, 1984, pp. 50-59.
- G. C. FOX, M. A. JOHNSON, G. A. LYZENGA, S. W. OTTO, J. K. SALMON, AND D. W. WALKER, Solving Problems on Concurrent Processors, Prentice-Hall, 1988.
- G. GOLUB AND C. VAN LOAN, Matrix Computations, Johns Hopkins University Press, Baltimore, 1983.
- J. L. GUSTAFSON, Reevaluating Amdahl's Law, Comm. ACM, 31, 1988.
- M. T. HEATH, ed., Hypercube Multiprocessors 1986, Society for Industrial and Applied Mathematics, Philadelphia, (1986).
- M. T. HEATH, ed., Hypercube Multiprocessors 1987, Society for Industrial and Applied Mathematics, Philadelphia, (1987).
- E. ISAACSON AND H. KELLER, Analysis of Numerical Methods, John Wiley & Sons, New York, 1966.
- G. R. MONTRY AND R. E. BENNER, Parallel processing on an ELXSI 6400, Proceedings of the 2nd International Conf. on Supercomputing, Vol. 2, ISI, Inc., St. Petersburg, FL, 1987, pp. 64-71.
- NCUBE Users Manual, Version 2.1, NCUBE Corporation, Beaverton, OR, 1987.
- Y. SAAD AND M. H. SCHULTZ, Data communication in hypercubes, Report YALEU/DCS/RR-428, Yale University, 1985.
- M. K. SEAGER, Parallelizing conjugate gradients for the CRAY X-MP, Parallel Computing, 3 (1986), pp. 35-47.
- C. L. SEITZ, The cosmic cube, Comm. of the ACM, 28 (1985), pp. 22-33.
- G. C. SZABO AND G. C. LEE, Derivation of stiffness matrices for problems in plane elasticity by Galerkin's method, International Journal of Numerical Methods in Engineering, 1, 1969, pp. 301-310.
Contact: John Gustafson
john.gustafson@sun.com
 2. Machine parameters specific to our hypercube system are summarized in
2. Machine parameters specific to our hypercube system are summarized in  3. A set of general algorithmic techniques used to achieve high parallel efficiency is described in
3. A set of general algorithmic techniques used to achieve high parallel efficiency is described in  4. Results for three applications on ensembles of up to 1024 processors are discussed in
4. Results for three applications on ensembles of up to 1024 processors are discussed in 
 5-7. Several advances in our understanding of parallel processing are summarized in
5-7. Several advances in our understanding of parallel processing are summarized in  8.
8.


 (N) to be the operation count for the best serial algorithm, where N is the size of the problem in one dimension. We also define
(N) to be the operation count for the best serial algorithm, where N is the size of the problem in one dimension. We also define 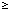
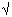 P). This operation cost is more work than would be performed by a serial processor:
P). This operation cost is more work than would be performed by a serial processor:
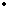
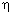 P(N) given by
P(N) given by
 1
1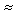 1020. An equivalent definition is the following: speedup is the sum of the individual processor efficiencies. Speedup shown in the graphs and tables in
1020. An equivalent definition is the following: speedup is the sum of the individual processor efficiencies. Speedup shown in the graphs and tables in 



 2
2 =
=  t)2
t)2


 t + (
t + (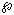 +
+ 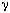 - 1)
- 1) 


 pk) - b(x0)) /
pk) - b(x0)) / 
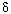 , then stop iteration loop timer and proceed with step C15. If iteration number i is a multiple of input parameter j and node number is 0, send inner products to host for monitoring progress of calculation.
, then stop iteration loop timer and proceed with step C15. If iteration number i is a multiple of input parameter j and node number is 0, send inner products to host for monitoring progress of calculation.
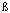 ].
]. 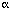 in the PCG algorithm (
in the PCG algorithm (