Computational Verifiability and the ASCI Program

John Gustafson

Ames Laboratory, USDOE

Abstract

The Advanced Strategic Computing Initiative is intended to replace the testing of nuclear weapons with computer simulations of those tests. This brings much-needed attention to an issue shared by all “Grand Challenge” computation programs: How does one get confidence, as opposed to mere guidance or suggestion, out of a computer simulation? There are ways to make the simulation of some physical phenomena rigorous and immune to the usual discretization and rounding errors, but these ways are computationally expensive and practiced by a vanishingly small fraction of the HPCC community. Some of the great increase in computing power proposed for ASCI should be placed not into brute force increases in particle counts, mesh densities, or finer time steps, but into the use of methods that place firm bounds on the range of the answer. This will put the debate over the validity of ASCI on scientific instead of political grounds.

Keywords: ASCI, chaos, computational science, integral equations, interval arithmetic, numerical analysis

1. Background

In 1996, the United Nations voted to adopt the Comprehensive Test Ban Treaty banning all nuclear testing, above ground or below ground, for peaceful purposes or military purposes [8]. Above-ground testing had been banned previously, but the three U.S. Department of Energy laboratories charged with weapons development and maintenance (Sandia National Laboratories, Los Alamos National Laboratories, and Lawrence Livermore National Laboratories) were able to verify and maintain the readiness of the nuclear arsenal (and improve existing designs) by means of underground testing. Now that all forms of testing are disallowed, there is a need for high-confidence computer simulation of every conceivable aspect of nuclear weapon behavior.

Computational science had its birth at Los Alamos in the 1940s, though the term was not used until Kenneth Wilson coined it in the mid-1980s. The accounts of the development of the first atomic bomb [2] mention the use of rooms full of mechanical calculators with operators following printed directions that effectively was a computer program. There was considerable interplay between the estimates made by calculators, the experiments performed, and the physical theory involved. It was the beginning of the use of computers as a third approach to doing science, complementing the experimental and the theoretical. I believe the following diagram is from Kenneth Wilson:

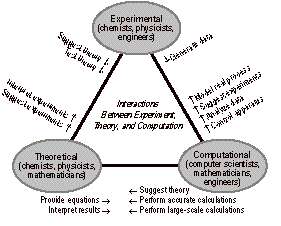
Fig. 1. The Role of Computational Science

Half a century later, we are putting so much stock into the computational approach that we can seriously consider eliminating the experimental component of the trio entirely. We do this not by choice, but by necessity. But this puts an additional burden on the computational side that forces us to a very different style of computing, one very few people have much experience with… one where results must be accompanied by guarantees. This is a new kind of science. Aristotle did experimentless science, but this is experimentless computational science, and as such may be without precedent.

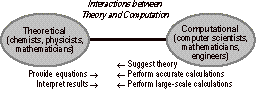
Figure 2. “Experimentless” Computational Science

2. The Sources of Error

If we assume that the theory is correct and complete for any physical simulation, then the main sources of error in what a computerized version of that theory produces are

• hardware failure,

• outright program bugs,

• discretization error, and

• rounding error.

Let’s examine each of these in the light of the ASCI program.

2.1. Hardware failure

If the mean time between failures (MTBF) of a processor-memory module is three years, then the MTBF of an ensemble of 9000 such modules can be no better than 3/9000 year, or about three hours. If a teraflop computer is limited to runs of about 3 hours (104 seconds), then its effective capability is to run simulations involving only about 1012 ops/sec ´ 104 sec = 1016 operations. This is far less than the number of operations used to crack RSA 129 two years ago, or to produce the movie Toy Story [4]]. Since the interconnection of the modules can be expected to produce many if not most of the hardware failures, the actual failure rate will be quite a bit higher than this estimate.

The users of business computers, IBM’s traditional stronghold, have long understood that reliability is a dimension of performance. Users of scientific computers tend to assume hardware reliability is perfect and need not concern them. But no matter how fast a computer is in terms of arithmetic operations per second, its performance will be very limited if it never stays up long enough to run a large problem. A slower but much more reliable system might actually have higher performance for this reason.

Arguments about the reliability of massively parallel computers tend toward one of two extremes:

• It’s so parallel, it can’t possibly work.

• It’s so parallel, it can’t possibly fail.

The first argument is ORing the failure possibilities, whereas the second one is ANDing them. If a system cannot tolerate single failures, then it is going to have trouble scaling to the sizes required by ASCI. If a system is designed to continue operating and allow hot-swapping of defective units, then it will be able to use its parallelism to enhance reliability instead of hurt it.

2.2 Bugs

Critics of ASCI contend that computer simulation will increase the problem of human error, long the bane of every program involving nuclear weapons. We have acquired a legacy of famous and spectacular bugs, for example, in the space programs of various countries. A missing comma causes a probe to crash on the surface of Venus, or a subtle program bug makes a worldwide flotilla of weather balloons self-destruct. Almost every year there is news of some human mistake amplified by the power of modern computers. As we get better at eliminating those mistakes, we take on more difficult and complex tasks such that the possibility of bugs again becomes limiting. Many pieces of commercial software now involve over a million lines of code, and the task set for ASCI is a superset of many existing programs in this complexity range.

No wonder, then that the dependence on computers required by ASCI makes some of us wary. One extreme is to say “It’ll never work,” and fight for resumed limited nuclear testing. Another extreme is to say, “Don’t worry, we’ll be careful,” and brush aside a problem that deserves our worry. A better engineering approach is to recognize human error as the omnipresent phenomenon that it is, and attempt to stay within the bounds of complexity we can manage instead of using ASCI to push the envelope to a new frontier. We must also be careful to maintain the attitude that bug-finders are to be rewarded, not punished; failure to do this is often the downfall of programs under intense pressure for perfection and success.

The budget for ASCI is not stingy; it stands at roughly $209 M per year presently, to be distributed primarily to the three DOE weapons laboratories, plus additional funding for university research. That funding should be sufficient to purchase many sets of eyes to look at the software, and there is nothing so effective for finding human errors as the scrutiny of one’s peers. For the discussion that follows, let’s assume that the errors from programming bugs have been factored out but that we still must deal with the fundamental verifiability of computer simulations.

2.3. Discretization Error

This is the error one gets from describing continuously varying quantities with discrete numbers one can represent on a computer. (This presumes, of course, that we are doing the simulations numerically instead of using a symbolic computer program like Mathematica® or Maple®.) Just to illustrate what discretization does to computer simulations, suppose we try to simulate a moon orbiting a planet with straightforward freshman physics methods.

If you provide initial positions and velocities that are exactly correct for circular orbit, and step the motions of the two bodies through time with discrete time steps, you might get an answer like this:

Fig. 3. N-Body Discretization Error

So the natural reaction is to think, “The time step is too large. Make it smaller.” And the trigger for this was that the answer looked wrong. The thing that will make the answer acceptable is when it looks right. Max Gunzburger calls this the “eyeball norm” for numerical analysis. If one did not know that it was a circular orbit but simply looked at the smoothness of the curves, would the following answer be accepted?

Fig. 4. More Subtle N-Body Discretization Error

It probably would. When the N-body problem is solved numerically for large N, errors far worse than this are probably committed. How many N-body programs are checked by testing them with N = 2 to see if a stable orbit is produced? Many N-body codes are used simply for qualitative information… watching galaxies collide, suggesting ways to focus charged particle beams, and so on. Other than solar system simulations, N-body code users do not usually care about exact positions of each particle. Discretization error does not prevent the computer simulation from providing useful guidance to experimentalists and theorists.

Whether finite element or finite difference methods are used, the management of discretization error is generally practiced as an art and not a science. Those with experience select subdivisions of time and space that they deem sufficient for the answers to be believable. Examination of numerical analysis textbooks reveals why: most state discretization errors using “O(…)” notation, for example,

Ñ2f0,0 = f–1,0 + f0,–1 + f1,0 + f0,1 – 4 f0,0 + O(h2)

So whatever the error is, one knows it varies as the square of the grid spacing, h. But it gives no absolute numerical information. If pressed, one can discover the more specific formula

Ñ2f0,0 = f–1,0 + f0,–1 + f1,0 + f0,1 – 4 f0,0 + 1⁄6 h2 f¢¢¢(x)

where x is some value in the range ±h from the given point. With nary a clue how to bound f¢¢¢(x), it is no wonder the management of computer error is treated as an art. “We don’t know what the discretization error is, but if we double the grid density then that error will decrease by a factor of four.” Failing a hard value for the error, one could examine the change in the answer as the grid density is varied and hope for answers that resemble asymptotic behavior. It would not be rigorous, but it would be persuasive if the functional form of the asymptote matched that predicted by the O(…) error terms. Where it fails is when other errors, such as rounding errors, contribute to the error and mask the discretization error.

2.4. Rounding Error

The prevailing attitude toward round-off error in floating-point arithmetic is to ignore it unless it becomes so spectacular that someone does the analysis to track it down. Mal Kalos, director of the Cornell Theory Center and no stranger to careful error analysis, has suggested that the ubiquity of the IEEE Floating Point Standard has made it possible to port programs from computer to computer without changing the answer in the least. In the Old Days, when one moved from a VAX to a CRAY to an IBM, the answer varied even when all three computers used “64-bit arithmetic.” Without that reminder of the approximate nature of computing, the IEEE answer becomes the “right” answer in the mind of users who should be more suspicious.

It is also much easier to get good performance with 64-bit precision, once considered a luxury. A common form of dilettante numerical analysis is to run a program in both single precision and double precision, and see if it matters. If it doesn’t, then single precision is deemed adequate. If it seems to give very different answers, then the single precision answers is deemed wrong and the double precision answer is deemed authoritatively correct.. Of course, it is not the least bit difficult to envision situations where none of the answers is “correct” to even two decimal places of accuracy, John von Neumann warned against using double precision to compensate for unstable calculations, saying, “If it’s not worth doing, it’s not worth doing well.”

Like discretization error analysis, round-off error analysis is depressingly difficult to do with rigor. If the reader thinks otherwise, try proving a bound on the round-off error involved in solving the quadratic equation ax2 + bx + c = 0 when a, b, and c, are approximated by IEEE 64-bit floating point values. The analysis can take many hours, and it leads one into distinctions between error in the input values and errors introduced by the computation. Many will be surprised to know that very large errors are possible even in a problem this simple, if the straightforward textbook formula is used. It doesn’t take a huge number of operations to accumulate significant round-off error; all it takes is one stumble. At a recent (April 1997) gathering of the three laboratories charged with ASCI, I saw a presentation of a declarative language that touted the ease with which parallelism could be extracted from it [6]. Solution of the quadratic equation was given as an example, and the example at no point recognized the pitfall of rounding error lurking in –b ± (b2 – 4ac)1/2. The speaker was unaware of the pitfall, and a personal poll afterward showed that only a few in the audience noticed.

But speaking of “huge numbers of operations,” the ASCI program suggests that systems capable of 1012 floating-point operations per second are needed initially (variously called 1 teraflop, 1 teraflop/s, or 1 TFLOPS), growing to 1015 floating-point operations in a few years (1 petaflop, 1 petaflop/s, or 1 PFLOPS). At these rates, even well designed programs may be pressed to get correct answers using merely 64-bit arithmetic. It is probably time for computer architects to revisit the issue of word sizes for arithmetic as they design computers with such high nominal speed. In running scalable benchmarks on the Intel Paragon at Sandia and the SP-2 at the Maui Supercomputer Center, I routinely run out of precision before I run out of memory. That is, progress in improving the quality becomes limited by 64-bit precision instead of the number of discretization points. Obviously, this is a function of the application under study; but the adequacy of 64-bit precision cannot be taken for granted on computers this fast.

3. Performance Goals and Moore’s Law

A phrase that appears over and over in ASCI proposals [7] is “100 trillion operations per second by 2004.” The derivation of this number is not explicit, but one can guess its origin. Assume a weapons code in current use on a computer rated at 10 billion operations per second. Assume it will be 100 times more difficult to do if made fully three-dimensional. Assume another factor of 100 to do “full physics” as opposed to simplified physics or physics involving only one type of phenomenon or time scale or spatial scale. Multiplying the factors, and assuming that the ratio of actual-to-rated speed on the computer remains the same, and one gets 100 ´ 100 ´ 10 billion = 100 trillion operations per second. A very similar argument is used in the estimates of computing power required to predict global climate change [1].

Attention to rounding and discretization errors could radically affect this estimate. The power needed for results we can trust might be much higher because of the extra work needed to make answers provably correct. However, it might also be too high; once the bounding of the answer is determined rigorously, it may turn out that far less arithmetic is needed to tighten the confidence intervals around the answers. The point is that we don’t know. The “100 trillion operations by the year 2004” becomes a mantra, and we forget to question where it comes from. ASCI will need to monitor that estimate and be prepared to change it as more is learned about the scaling of the algorithms and their associated error terms.

Another item worth noting is that the “A” in “ASCI” refers to “Accelerated.” Compared to what? Compared to Moore’s law! Moore’s law notes that semiconductor technology increases density and reduces price by a factor of two every eighteen months. This exponential curve fit can be applied to processor or memory technology. For processor technology, the curve fit is not very accurate; processor density and performance shows fits and starts and plateaus in its history since the Intel 4004 was introduced. For one thing, the measure of “performance” of a processor has been and remains elusive.

On the other hand, Moore’s law is extremely accurate in predicting memory technology. Bits per DRAM chip have quadrupled inexorably about every three years, despite a number of attempts to accelerate the process. There is a collision between the demands of ASCI and the evidence that memory density and price can only improve at the rate we’ve seen for the last 27 years. If the demands of the huge international market for denser and cheaper memory cannot accelerate Moore’s law for memory chips, why would a $0.2 billion/year federal program be able to do so?

To resolve this, there are two ways out:

1. Assume that we will accelerate the spending beyond the usual inflation applied to supercomputer prices so that each system has more memory than would be predicted by Moore’s law.

2. Assume that the ratio of operations to storage increases. Amdahl’s original guideline of “One megaflop per megaword of memory” has been bent to “one megaflop per megabyte of memory” as megaflops have become much cheaper for designers to increase than megawords. The initial configuration of the 9000-processor teraflop computer at Sandia intended for ASCI has a terabyte of disk storage, and considerably less than that in addressable RAM.

The first assumption is not amenable to scientific discussion, other than to note that megacomputer sizes have historically been limited as much by physical size and parts count as by cost. Infinite money does not buy an infinitely fast computer; other factors intrude.

Is the second assumption valid? There is a very convincing argument that the ratio of operations to variables increases with problem size. In other words, operation complexity is a superlinear function of storage complexity. If one improves the spatial resolution of a simulation, one will need more timesteps and hence more operations per data item. “Full physics” similarly involves more computations per data item. For purposes of ASCI, therefore, we may indeed be able to get away with low amounts of memory compared to the historical proportion to the arithmetic speed.

As conventional workstations have grown in power, however, where the users have considerable control over the amount of memory they configure, the systems gravitate toward the ratio of one word for every operation-per-second delivered. A single-user computer capable of 8 megaflops probably has at least 64 megabytes (8 megawords, that is) of RAM. The earliest IBM-compatible PCs could deliver perhaps 40 kiloflops, and yet quickly grew to the 640-kilobyte limit imposed by the original system design. The reason seems to be that these computers spend considerable time on applications where there really is a linear relationship between operations and storage. Editing is one example. Almost any application involving money is another. Sorting operations may increase the work to order N log N for order N items, which is practically the same as a linear relationship between work and storage.

A system is balanced when its users are equally frustrated by the size of the problem they can run and the time it takes to run problems of that size. If users run out of patience, then the system has too much memory for its arithmetic speed. If the users run out of space, then the system is too fast for the amount of memory it has. Only time will tell, but full three-dimensional physics cases seem likely to burden the arithmetic more than the storage. This is how ASCI may be able to surpass the drumbeat of Moore’s law.

4. Chaos

Many differential equations, especially those with damping terms, can be unstable everywhere. The instability does not disappear with increased numerical precision. It is quite possible to go through a thorough training in the applied sciences and never learn about chaotic behavior. Here again, the methods used to make decisions are graphical and unrigorous; operators of a computer program notice that results look like discontinuous functions of the input assumptions. When chaotic behavior was first observed in weather simulations and other modeling programs, it was invariably dismissed as a computer error of some kind [3].

Imagine an ASCI simulation in which the space of input assumptions is not sufficiently explored by even minute changes. The answer could well lie in a chaotic region without being detected as such. The computer creates false confidence in the answer, since we all have been trained to expect continuous behavior in natural phenomena. This is one area where the quest for raw speed in operations per second is legitimate; the speed can be used to run many variations of a simulation with perturbations to detect chaos or other numerical instabilities. The only thing missing is a widespread awareness of the need to do so. This brings us to the issue of education.

5. Education

The ASCI program will have a large appetite for people expert in these issues: controlling incidences of bugs, discretization error, and round-off errors. Where will it get them? Not from the current crop of computer science graduates.

At ISU and most other schools, I can ask a class of 25 computer science graduate students, “How many of you have had a course in numerical analysis?” and get not one hand raised. “How many of you have written a computer program more than 10 pages long?” gets a similar result. I’m more likely to find extensive programming experience in a physics or chemistry student who is self-taught as a side-effect of the computing effort entailed in dissertation work. In computer science curricula, the study of complexity theory, finite automata, and Turing Machines leaves little time for hands-on software engineering. Computer science departments are often ensconsed in Liberal Arts programs, and inherit a natural aversion to any teaching that smacks of trade school apprenticeship.

One hopes that the pressure of ASCI will have the desirable side effect of raising awareness of the need for computational science and software engineering programs in U.S. colleges. Currently it is difficult even to find professors qualified to teach courses for such programs. The bottom right oval of Figure 1 is not going to be properly staffed unless the “computer scientists” coming out of U.S. colleges know how to create and maintain very large programs that work.

6. Reviving Rigor

In the 1980s, there was a resurgence of interest in “interval arithmetic.” In its simplest form, one keeps two floating-point values for every quantity that bracket the value being represented. For every operation, worst-case reasoning is applied to update the bounds. Since this can be handled automatically by the computer, it amounts to a “Round-Off Error For Dummies” method. It can, for instance, flag potential disasters in the quadratic equation problem mentioned previously. But it has at least three shortcomings: First, it doesn’t give constructive advice when error bounds become too large. Second, the error bounds are overly conservative; they quickly grow to [–¥, ¥] (as represented by the computer). Users notice that their answers seem to be much better than the worst-case analysis, and cease to regard the interval bounds as having any value. Third, interval arithmetic is expensive since it takes twice the storage and at least twice the work of ordinary arithmetic. It is a classic tradeoff between speed and answer quality.

A recurring theme in the history of computing is that speed is initially thought of as a way to reduce time, but eventually becomes a way to improve answer quality in the time people are willing to wait (which is roughly constant). When IBM developed its first laser printers, they envisioned a replacement for their line printers that would spew out three pages per second. Restricted to block capital letters, laser printers were easily capable of such speed in 1977, just as they are twenty years later. But instead we use the speed to increase output quality, and still wait many seconds per printout as before. Massively parallel computers perform poorly at reducing time for existing serial tasks, but they are a godsend for solving problems far too large for serial computers… in about the same time as the serial task takes to run on the serial computer. Perhaps it is time for us to roll some of the teraflops - petaflops performance improvements into methods that greatly increase the answer quality, even if it means using a completely new approach.

There were major advances in interval arithmetic in the 1980s [5]. Researchers at IBM in West Germany found ways to keep the bounds from growing beyond one unit of least precision (ULP) for basic block sections of computer programs. This found commercial application in PASCAL-SC and ULTRITH, now all but forgotten forays into round-off error control. PASCAL-SC was approximately 100,000 times slower than straight PASCAL, a hefty price to pay for the elimination of uncertainty. It could be used on small programs to verify the validity of an approach, but straight PASCAL used once the approach appeared sound. It’s worth noting that advances in computer speed since they days of PASCAL-SC are probably approaching a factor of 100,000… hence one can now run production problems from the mid-1980s at about the same speed but with confidence in the control of round-off error. Germany, specifically the University of Karlsruhe, remains the center of activity on interval arithmetic and verifiable numerical computation. We would do well to echo the fervor of the Germans in the ASCI program.

7. The Last Frontier of Validity: Bounding Discretization Error

Of the three sources of error described here, discretization error is the one most likely to be approached using brute force, i.e., use more flops/second to refine the grid or raise the polynomial order of the approximation. ASCI is no exception. (Another clear example of this is the CHAMMP proposal for climate prediction, which demands a 104 increase in speed to increase the grid spacing, time stepping, and physical completeness in climate models [1]). It is often arguable that current grids are too coarse, that particle counts are too small, that time steps are too large (see the 2-body example above) for a computer model to be a good approximation of the truth. What is much harder to argue is what level of resolution or problem “size” will create acceptable accuracy. “Infinite!” is not a good answer, nor is it one likely to attract support from cognizant managers of research programs.

Here, then, is a general approach for physical simulation programs that may help (at least for problems where the physics is not terribly complex):

Using arguments from physics (like causality, and the conservation of energy, momentum, and mass) and mathematics (like the Mean Value Theorem and provable inequalities for integrals), ask what is the smallest and largest every calculated value can be. Then write the computer program to calculate those bounds instead of the usual best guess. If the bounds are too loose, either improve computer speed or the reasoning that produces the bounds.

This is like interval arithmetic, but for discretization error instead of round-off error. It attacks the weakest link in the chain from problem concept to numerical answer: the approximation of continuum physics by discrete variables. Some examples of this approach follow.

7.1. Example: Radiation Transfer

A closed geometry is described by polygons that reflect radiation; some of the polygons also emit radiation. The reflectance ranges from 5% to 95%, say. Each polygon i gives off radiation bi(r), where r is the position on the polygon. This amount represents what the patch is emitting, ei(r), plus what it is reflecting as the result of receiving radiation from the total of all other sources. That radiation from patch j reaching point r is described by an integral,

∫S F(r, r¢) bj(r¢) dr¢

where F is the “coupling factor,” which can be thought of as the fraction of the radiation from r¢ that reaches r. The “radiosity problem,” is to find the equilibrium radiation transfer:

bi(r) = ei(r) +ri ∫S F(r, r¢) bj(r¢) dr¢

To apply the reasoning given above, initially consider what is the minimum possible radiation given off by every polygon. That would be if somehow all couplings to other polygons were zero, so only emitted radiation is given off (no reflected radiation). bmini = ei. The other extreme, the maximum radiation given off by every polygon would be if all the reflectances were the maximum reflectance, 0.95, causing emitted sources to be reflected as the sum of the infinite series 0.95 + 0.952 + 0.953 + … = 1⁄(1–0.95) = 20. So an initial bound on the radiosity of every polygon is [ei, ri(20emaxi)].

The iterative process can now monotonically improve this conservative bound. Gauss-Seidel iteration (without over-relaxation) will bring the upper bound down and the lower bound up monotonically. The coupling factors are themselves expressed by integrals, and can be bounded above and below. By this method, I have obtained rigorous bounds for particle transport flux that can be applied to visible photons for graphics or to the motion of neutrons and high-energy photons in a nuclear device. At each stage, one applies physical limiting principles: What is the most radiation that could transfer from surface i to surface j? What is the least radiation that could make be transferred?

This approach can be combined with interval arithmetic to control rounding error. Support for rounding control is weak or nonexistent in present programming languages, though rounding control is provided in the IEEE floating-point standard. Perhaps the magnitude of the ASCI project will change programming languages; a language extension would greatly help the rigorous bounding of answers.

7.2. Integral Equations

What makes the preceding example possible is the formulation of the problem as an integral equation, not a differential equation. Here again there is a problem with the existing paradigm. A technical education in the U.S. puts strong emphasis on differential equations, often requiring a full semester in it, yet integral equations are given barely a passing mention.

Integrals are numerically well-behaved. They can be bounded rigorously or computed by Monte Carlo methods with analyzable statistical error. Derivatives are just the opposite; they are badly behaved. Estimating derivatives with finite differences immediately sets up a tradeoff between rounding error and discretization error, and bounding either one may be very difficult. More to the point, either error may be quite large.

Many problems traditionally expressed as differential equations may be reformulated as integral equations. I mean this not just in the vacuous sense of redefining the highest-order derivative as the function to be found and the lower-order derivatives as integrals of that unknown function, but as a more direct path from the actual physics to the computer simulation. If we teach ourselves to look for accumulated quantities and not rates in the transcription of the physics, we may eventually find integral equations a more natural way to express the behavior of nature. The use of discrete computer arithmetic can then give us everything we want in simulating that behavior. We may have to dust off some century-old mathematical treatises on integral equations, but we probably don’t have to do much original thinking. It’s simply a different choice in the formulation.

Summary

“Performance” has many dimensions when applied to computing, and we have tended to focus on the operations-per-second dimension. When confronted with a particularly arduous computing problem, it is easy to make the mistake of couching the goal in terms of teraflops or petaflops. The goal for which we need high performance, in both ASCI and in most kinds of scientific computing, is the reduction of uncertainty in predictive statements. For that one needs hardware reliability, software reliability, and rigorous numerical analysis. One also needs programmers and users aware of (though not necessarily expert in) chaos theory and interval bounding methods so that the computer can completely replace experiment and not merely supplement it as has been done up to now.

If we can place more emphasis on these other aspects of “performance” in the formative years of the program, I believe we can increase the chances that ASCI will succeed.

References

[1] Computer Hardware, Advanced Mathematics, and Model Physics (CHAMMP) Pilot Project Final Report, U.S. DOE Office of Energy Research, DOE/ER-0541T Dist. Category 402, May 1992.

[2] James Gleick, Genius: The Life and Science of Richard Feynman, Pantheon Press, New York, 1992.

[3] James Gleick, Chaos, Penguin Books, New York, 1987.

[4] John Gustafson, The Program of Grand Challenge Problems: Expectations and Results, The Second Aizu International Symposium on Parallel Algorithms/Architecture Synthesis, March 17-21, 1997, Fukushima, Japan, IEEE Computer Society Press, 1997.

[5] Interval arithmetic information can be found at http://cs.utep.edu/interval-comp/main.html

[6] Ajita John, “Parallel Programs from Constraint Specifications,” presented at The Conference on High Speed Computing, LLNL/LANL, Salishan Lodge, Gleneden Beach, Oregon, April 21–24, 1997.

[7] King Communications Group, “Don’t Blow Hot and Cold on ASCI,” HPCC Week, Washington DC, March 27, 1997.

[8] U.S. Department of Senate, Daily Press Briefing, DOT #147, September 11, 1996.

___________

PROF. JOHN GUSTAFSON is a Computational Scientist at Ames Laboratory in Ames, Iowa, where he is working on various issues in high-performance computing. He has won three R&D 100 awards for work on parallel computing and scalable computer benchmark methods, and both the inaugural Gordon Bell Award and the Karp Challenge for pioneering research using a 1024-processor hypercube. Dr. Gustafson received his B.Sc. degree with honors from Caltech and M.S. and Ph.D. degrees from Iowa State, all in Applied Mathematics. Before joining Ames Laboratory, he was a software engineer for the Jet Propulsion Laboratory in Pasadena, Product Development Manager for Floating Point Systems, Staff Scientist at nCUBE Corporation, and Member of the Technical Staff at Sandia National Laboratories. He is a member of IEEE and ACM.

Errata: In January 1999, I was contacted by the original author of Pascal SC, Prof. Dr. Juergen Wolff v. Gudenberg, regarding the figure of 100,000 given as the slowdown ratio in Section 6. He believes the ratio was never worse than 100. Since I cannot find my original reference for the 100,000 number and a figure of 100 seems more plausible, I defer to his correction! — Author