Last November, we introduced in these pages a new kind of computer benchmark: a complete scientific problem that scales to the amount of computing power available and always runs in the same amount of time--one minute. SLALOM assigns no penalty for novelty in language or architecture, and runs on computers as different as an Alliant, a MasPar, an NCUBE and a Toshiba notebook PC.
Since that time, there have been several developments:
We're still waiting to hear results for a few major players in supercomputing: Thinking Machines, Convex, MEIKO and Stardent haven't sent anything to us, nor have any of their customers. We'd also very much like numbers for the WaveTracer and Active Memory Technology computers. Our Single-Instruction, Multiple Data (SIMD) version has been improved since the last Supercomputing Review article, so the groups working on those machines might want to check it out as a better starting point (see inset). The only IBM mainframe measurements are nonparallel and nonvector, so we expect big improvements to its performance.
We're awaiting word from the Japanese computer makers: NEC, Hitachi Data Systems and Fujitsu. We also welcome entries from small systems. Anything over 137 FLOPS should be able to finish a small run in less than 60 seconds.
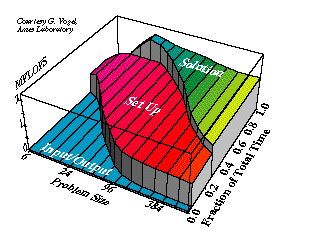
A marvelous thing happens with fixed-time benchmarking, not mentioned in our previous report. Many parallel machines more than double their MFLOPS rate when they double the number of processors used. The reason for this is illustrated by the figure below:

Most scientific computers achieve their highest MFLOPS rate doing matrix operations, and lower MFLOPS rate doing setup and miscellaneous tasks. Input/output might not score any MFLOPS at all! As the problem size grows, the matrix operations become a larger and larger fraction of the one-minute run, so the average speed per processor increases. One reason the MFLOPS entries in the table increase so nicely when the number of processors increases is because this effect compensates for some of the usual losses of parallel efficiency.
This is one reason one shouldn't use MFLOPS (or MIPS) to measure performance, of course. Right now we provide MFLOPS in the table to help people translate the performance to something for which they have a feel, but ultimately the only number that matters is the size of the problem solved, here measured by the number of patches.
To answer one question we've been asked repeatedly, we will not accept money in return for optimizing SLALOM performance. But we will provide, for free, unbiased advice and suggestions to anyone trying to get the best possible performance out of their system.
We also do not allow use of these results in advertising without our prior consent. Too often, benchmark data has been "excerpted" in lists that conveniently eliminate certain competing machines or crucial footnotes that tell the full story. If you suspect that SLALOM information is being misused, please contact us immediately. SLALOM is designed to resist "benchmark rot," and we'll fight to preserve its integrity.
A bit of folklore in this business goes something like this: "Half the improvements in computing speed come from hardware advances, and the other half come from algorithm advances." That is, if an application runs 10^8 times faster than it did 35 years ago, it's probably the result of 10^4 times faster hardware and 10^4 times faster algorithms. Starting in 1990, SLALOM began what may be a decades-long experiment to test this aphorism.
At Cray Research, Inc. and elsewhere, a technique known as Strassen multiplication was used in the matrix solver. The idea is that 2 by 2 matrix multiplication can be done with 7 multiplications rather than the usual 23 = 8, and this can be applied recursively to n by n matrices to allow general matrix multiplication in order n^log27 (about n^2.8) floating-point operations. More recent methods take the exponent down as low as 2.4, but are only advantageous for very large n. So we now have "blocked" versions of SLALOM that use matrix-matrix multiplication as the kernel (similar to LAPACK), and you can adjust the size of the matrix and the method used to whatever works best. That was the first major improvement to the SLALOM algorithm.
James B. Shearer, of the IBM T.J. Watson Research Center, has provided a number of ideas for SLALOM, especially in the "SetUp" routines. He discovered a way to reduce the number of calls to the logarithm function, and found ways to re-use some quantities without loss of generality. For very large numbers of patches, he points out, the rounding error in our coupling function will make mathematically approximate formulas computationally more accurate. Fortunately, that will offer only a slight improvement because the setup is only a small part of the one-minute run for such large numbers of patches.
Shearer also suggests that iterative methods for solving the matrix will beat our direct method, at least for the suggested input data. He may be right, but we reserve the right to evaluate systems based on their worst-case-input behavior. If all the walls in the radiosity problem are highly reflective, iterative methods converge very slowly. But we invite the experiment.
These algorithm improvements are another reason not to use MFLOPS to compare performance. These improvements might allow larger problems without higher MFLOPS, and post-mortem operation counts are very difficult with these clever optimizations. For now, we will continue to estimate the minimal operations for the best serial version of the program, which will be accurate to a few percent in most cases.
SLALOM will absorb these changes and others that arise. An upper bound on advances occurs if finer problem decomposition yields no improvement in answer accuracy, for some problem size that can be solved in less than a minute on some machine. This would mean the end of the rate for this first SLALOM experiment, and we would seek different scalable problems on which to base a fixed-time performance comparison. But for now, the SLALOM benchmark looks like it may last for a while.
| The SLALOM Benchmark Report | ||||||||
|---|---|---|---|---|---|---|---|---|
| The following list ranks computers that are actively marketed | ||||||||
| Computer, environment | Processors | Patches | Measurer | Date | ||||
| Cray Y-MP8, 167 MHz Fortran+tuned LAPACK solver (Strassen) |
8 | 5120 | J. Brooks (v) Cray Research |
9/21/90 | ||||
| Cray Y/MP-4, 167 MHz Fortran+tuned LAPACK solver (Strassen) |
4 | 4096 | J. Brooks (v) Cray Research |
9/21/90 | ||||
| nCUBE 2, 20 MHz Fortran+assembler |
1024 | 3720 | J. Gustafson Ames Lab |
1/11/91 | ||||
| Cray Y/MP-2, 167 MHz Fortran+tuned LAPACK solver (Strassen) |
2 | 3200 | J. Brooks (v) Cray Research |
9/21/90 | ||||
| Cray Y/MP-1, 167 MHz Fortran+tuned LAPACK solver (Strassen) |
1 | 2560 | J. Brooks (v) Cray Research |
9/21/90 | ||||
| nCUBE 2, 20 MHz Fortran+assembler |
256 | 2493 | J. Gustafson Ames Lab |
1/11/91 | ||||
| Cray-2S/8, 244 MHz Fortran+directives FPP 3.00Z25 |
8 | 2443 | S. Elbert Ames Lab |
9/8/90 | ||||
| Intel iPSC/860, 40 MHz, Fortran+assembler BLAS (pgf77 -03 NOIEEE) |
64 | 2167 | T. Dunigan ORNL |
1/7/91 | ||||
| MasPar MP-1, 12.5 MHz C with plural variables (mpl) |
16384 | 2047 | J. Brown (v) MasPar |
11/20/90 | ||||
| iPSC/860, 40 MHz Fortran (-O3 -Knoieee) |
32 | 1920 | E. Kushner (v) Intel |
1/25/91 | ||||
| MasPar MP-1, 12.5 MHz, C with plural variables (mpl) |
8192 | 1791 | M. Carter Ames Lab |
1/15/91 | ||||
| Alliant FX/2800 Fortran (-Ogc, KAI Lib's) |
14 | 1736 | J. Perry (v) Alliant |
1/24/91 | ||||
| iPSC/860, 40 MHz Fortran (-O3 -Knoieee) |
16 | 1671 | E. Kushner (v) Intel |
1/25/91 | ||||
| nCUBE 2, 20 MHz Fortran+assembler |
64 | 1623 | J. Gustafson Ames Lab |
4/8/91 | ||||
| nCUBE 2, 20 MHz Fortran+assembler |
64 | 1598 | J. Gustafson Ames Lab |
1/11/91 | ||||
| Alliant FX/2800 8 Fortran (-Ogc, KAI Lib's) |
8 | 1502 | J. Perry (v) Alliant |
1/24/91 | ||||
| MasPar MP-1, 12.5 MHz C with plural variables (mpl) |
4096 | 1470 | M. Carter Ames Lab |
1/14/91 | ||||
| Intel iPSC/860, 40 MHz Fortran+assembler BLAS (pgf77 -O3 NOIEEE) |
16 | 1404 | T. Dunigan ORNL |
1/7/91 | ||||
| iPSC/860, 40 MHz Fortran (-O3 -Knoieee) |
8 | 1392 | E. Kushner (v) Intel |
1/25/91 | ||||
| Silicon Graphics 4D/380S 33 MHz, Fortran+block Solver (-O2 -mp) |
8 | 1308 | O. Schreiber (v) Silicon Graphics |
1/28/91 | ||||
| IBM RS/6000 540, 30 MHz Fortran+ESSL calls XLF V2 prerelease, -O |
1 | 1304 | J. Shearer (v) IBM |
1/8/91 | ||||
| FPS M511EA, 33 MHz Fortran+LAPACK calls f77 -Oc vec+ -Oc inl+ |
1 | 1197 | B.Whitney (v) FPS Computing |
1/24/91 | ||||
| Alliant FX/2800 Fortran (Ogc DAS -KAI Lib's) |
4 | 1139 | J. Chmura (v) Alliant |
12/7/90 | ||||
| MasPar MP-1, 12.5 MHz, C with plural variables (mpl) |
2048 | 1119 | M. Carter Ames Lab |
1/15/91 | ||||
| iPSC/860, 40 MHz Fortran (-O3 -Knoieee) |
4 | 1103 | E. Kushner (v) Intel |
1/25/91 | ||||
| IBM RS/6000 520, 20 MHz Fortran+ESSL calls, XLF V2 , prerelease -O |
1 | 1091 | J. Shearer (v) IBM |
1/9/91 | ||||
| Silicon Graphics 4D/380S 33 MHz, Fortran+block Solver (-O2 -mp) |
4 | 1065 | O. Schreiber (v) Silicon Graphics |
1/28/91 | ||||
| nCUBE 2, 20 MHz Fortran+assembler |
16 | 994 | J. Gustafson Ames Lab |
1/11/91 | ||||
| MasPar MP-1, 12.5 MHz C with plural variables (mpl) |
1024 | 927 | J. Brown (v) MasPar |
10/5/90 | ||||
| Intel iPSC/860, 40 MHz Fortran+assembler BLAS (pgf77 -O3 NOIEEE) |
4 | 905 | T. Dunigan ORNL |
1/7/91 | ||||
| IBM RS/6000 320, 20 MHz Fortran+block Solver (-O -lblas, some -qopt=3) |
1 | 895 | S. Elbert Ames Lab |
1/30/91 | ||||
| Silicon Graphics 4D/380S 33 MHz, Fortran+block Solver (-O2 -mp) |
2 | 834 | S. Elbert Ames Lab |
1/30/91 | ||||
| SKYbolt, 40 MHz i860/i960 C+assembler dot product (-O sched vec UNROLL) |
1 | 831 | C. Boozer (v) SKY Computers |
1/9/91 | ||||
| SKYstation, 40 MHz i860/i960 C (-O sched vec UNROLL) |
1 | 793 | C. Boozer (v) SKY Computers |
1/29/91 | ||||
| Silicon Graphics 4D/35 37 MHz, Fortran, (-O2 -mp) |
1 | 717 | O. Schreiber (v) Silicon Graphics |
1/29/91 | ||||
| Alliant FX/2800 Fortran (Ogu -KAI Lib's) |
1 | 693 | J. Chmura (v) Alliant |
12/7/90 | ||||
| Silicon Graphics 4D/380S 33 MHz, Fortran+block Solver (-O2) |
1 | 676 | S. Elbert Ames Lab |
1/30/91 | ||||
| IBM 3090-200VF Fortran (Fortvs2n) Unvectorized |
1 | 657 | R. Hollebeek U. Penn |
11/29/90 | ||||
| iPSC/860, 40 MHz Fortran (-O3 -Knoieee) |
1 | 647 | E. Kushner (v) Intel |
1/25/91 | ||||
| FPS-500 (33 MHz MIPS + vec. unit) Fortran (FPS F77 4.3,-Oc vec) |
1 | 619 | P. Hinker LANL |
11/12/90 | ||||
| nCUBE 2, 20 MHz Fortran+assembler |
4 | 596 | J. Gustafson Ames Lab |
1/11/91 | ||||
| DECStation 5000, 25 MHz Fortran+block Solver (-O2) |
1 | 534 | S. Elbert Ames Lab |
1/30/91 | ||||
| Silicon Graphics 4D/25, 20 MHz Fortran+block Solver (f77 -O2) |
1 | 507 | S. Elbert Ames Lab |
1/30/91 | ||||
| DECStation 5000 25 MHz, Pascal (-O2) |
1 | 432 | D. Rover Ames Lab |
1/31/91 | ||||
| SUN 4/370, 25 MHz C (ucc -O4 -dalign etc.) |
1 | 419 | M. Carter Ames Lab |
10/8/90 | ||||
| DECStation 3100, 16.7 MHz Fortran+block Solver (-O2) |
1 | 418 | S. Elbert Ames Lab |
1/30/91 | ||||
| Sil. Graphics 4D/20, 12.5 MHz Fortran+block Solver (f77 -O2) |
1 | 401 | S. Elbert Ames Lab |
1/30/91 | ||||
| DECStation 2100, 12.5 MHz Fortran+block Solver (-O2) |
1 | 377 | S. Elbert Ames Lab |
1/30/91 | ||||
| nCUBE 2, 20 MHz Fortran + assembler subroutines (-O2) |
1 | 354 | J. Gustafson Ames Lab |
8/13/90 | ||||
| DECStation 2100, 12.5 MHz, C (cc -O3) |
1 | 340 | M. Carter Ames Lab |
1/24/91 | ||||
| Motorola MVME181, 20 MHz Fortran, (OASYS F77 1.8.5) |
1 | 289 | R. Blech NASA |
10/17/90 | ||||
| Sequent Symmetry 33 MHz C (cc -O -fpa) |
1 | 253 | M. Carter Ames Lab |
1/3/91 | ||||
| VAXStation 3520 C (cc -O) |
1 | 181 | M. Carter Ames Lab |
1/24/91 | ||||
| Cogent XTM (T800 Transputer) Fortran 77 (-O -u) |
1 | 149 | C. Vollum (v) Cogent Research |
6/11/90 | ||||
| Toshiba 1000, 6 MHz 8088 C (Turbo C, with reg/jump option) |
1 | 12 | P. Hinker LANL |
11/14/90 | ||||
A "(v)" after the name of the person who made the measurement indicates a vendor. Vendors frequently have access to compilers, libraries, and other tools that make their performance higher than that achievable by a customer.
The CRAY Y-MP runs failed the old SetUp3 tolerance of 5.E-10, but passed with a tolerance of 5.E-8; special LOG and ATAN functions were used with only 11-decimal precision for higher speed. We will enforce the current tolerance uniformly in our next report.
The CRAY 2 figures are low because blocking methods were not used; future runs will use matrix-matrix multiply as the kernel, as was done for the Y-MP.
Contact: John Gustafson