Abstract
A popular argument, generally attributed to Amdahl [1], is
that vector and parallel architectures should not be carried to extremes
because the scalar or serial portion of the code will eventually dominate.
Since pipeline stages and extra processors obviously add hardware cost, a
corollary to this argument is that the most cost-effective computer is one
based on uniprocessor, scalar principles. For architectures that are both
parallel and vector, the argument is compounded, making it appear that
near-optimal performance on such architectures is a near-impossibility.
A new argument is presented that is based on the assumption
that program execution time, not problem size, is constant for
various amounts of vectorization and parallelism. This has a dramatic effect on
Amdahl’s argument, revealing that one can be much more optimistic about
achieving high speedups on massively parallel and highly vectorized machines.
The revised argument is supported by recent results of over 1000 times speedup
on 1024 processors on several practical scientific applications [2].
1.
Introduction
We begin with a review of Amdahl’s
general argument, show a revision that alters the functional form of his
equation for speedup, and then discuss consequences for vector, parallel, and
vector-parallel architectures. [Vector and multiprocessor parallelism can be
treated uniformly if pipeline stages are regarded as independent processors in
a heterogeneous ensemble.] The revised speedup equation is supported with
recent experimental results for fluid mechanics, structural analysis, and wave
mechanics programs. We then argue that the conventional approach to
benchmarking needs revision because it has been based on Amdahl’s paradigm.
2.
Fixed-Sized Problem Model
Suppose that a program executes on a
scalar uniprocessor in time s + p,
where s is the portion of the time spent in serial or scalar parts
of the program, and p is the portion of the time spent in
parts of the program that can potentially be pipelined (vectorized) or run in
parallel. For algebraic simplicity, we set the program run time to unity so
that s + p = 1. Figure 1
shows the effect on run time of using an architecture that has vector or
parallel capability of a factor of N on the p
portion of the program.
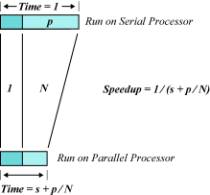
Figure 1. Fixed-Sized
Model (Amdahl’s Argument)
The figure makes obvious the fact that
speedup with these assumptions can never exceed 1 ŕ s even
if N is infinite. However, the assumption that the problem is fixed
in size is questionable. An alternative is presented in the next
section.
3. Scaled
Problem Model
When given a more powerful processor, the
problem generally expands to make use of the increased facilities. Users have
control over such things as grid resolution, number of time steps, difference
operator complexity, and other parameters that are usually adjusted to allow
the program to be run in some desired amount of time. Hence, it may be most
realistic to assume that run time, not problem size, is constant.
As a first approximation, we assert that
it is the parallel or vector part of a program that scales with the problem
size. Times for vector startup, program loading, serial bottlenecks, and I/O
that make up the s component of the run do not grow with problem size (see
experimental results below). As a result, the diagram corresponding to Figure 1
for problems that scale with processor speed is shown in Figure 2.
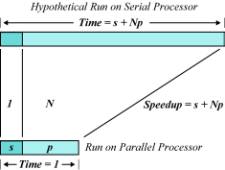
Figure 2. Scaled Model Speedup
It could well be that the new problem cannot actually be
run on the serial processor because of insufficient memory, and hence the time
must be extrapolated. Rather than ask, “How long will the current-sized problem
take on the parallel computer?” one should ask, “How long would the new
problem have taken on the serial computer?” This subtle inversion of the comparison
question has the striking consequence that “speedup” by massive parallelism or
vectorization need not be restricted to problems with miniscule values for s.
Architectures like hypercubes have memory distributed over
the ensemble, so that a problem appropriate for a 1024-node hypercube would
exceed the memory capacity of any one node by a factor of 1024. The simplest
way to measure “speedup” on such a system is to measure the minimum efficiency
of any processor (computation versus interprocessor communication overhead) and
multiply by the number of processors.
In striving for high efficiency, the functional form s + Np is far more forgiving
than Amdahl’s 1 ŕ (s + p ŕ N), as illustrated in Figure 3 for N = 64.
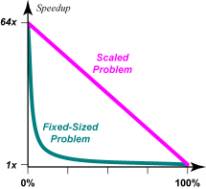
Figure 3. Scaled versus Fixed-Sized Speedup
Figure 3 applies whether we are dealing
with a 64-processor system or a vector computer with 64-stage pipelines (64
times faster vector performance than scalar performance, similar to the ratio
for memory fetches for the CRAY-2).
Note in particular the slope of
the graph at s = 0 in Figure 3. For Amdahl’s fixed-sized
paradigm, the slope is
d(speedup) ŕ ds |s = 0 = N – N 2 (1)
whereas for the scaled paradigm the slope
is a constant:
d(speedup) ŕ ds |s = 0
= 1 – N (2)
Comparison of (1) and (2) shows that it
is N times “easier” to achieve highly-vectorized or
highly-parallel performance for scaled-sized problems than for constant-sized
problems, since the slope is N times as steep in Amdahl’s
paradigm.
4.
Experimental Results
At Sandia, we have completed a study of
three scientific applications on a 1024-node hypercube [2]. The applications
are all scalable by the number of time steps and grid resolution
(finite-element or finite-difference). We measured speedup by the traditional
technique of fixing the problem size and also by scaling the problem so that
execution time was constant. The resulting speedups are as follows:

By careful management of the parallel
overhead, all three applications showed speedups of several hundred even when a
fixed-sized problem was spread out over 1024 processors (i.e.,
using 0.1% of available memory). However, as the global problem size was scaled
to the number of processors (i.e., fixing the problem size per
processor), the p portion of the problem grew linearly with the number of
processors, N. Specifically, at N = 1024 we
measured the increase in p to be 1023.9959 for the Beam
Stress Analysis, 1023.9954 for Baffled Surface Wave Simulation, and 1023.9965
for Unstable Fluid Flow. Deviation from 1024 was caused primarily by small
terms that grow as log N.
When Amdahl’s Law is applied to the
results of [2], it shows that four-hour runs were reduced to 20-second runs, of
which about 10 seconds was caused by s and cannot be much
further improved. But when run time is fixed by scaling the problem, the
speedups indicate very little reason why even more massive
parallelism should not be attempted.
5.
Combination Vector-Parallel Architectures
It is perhaps worth repeating that
pipelining is a form of parallelism. As an example, Figure 4 shows a simplified
diagram of an array processor and a low-order hypercube.
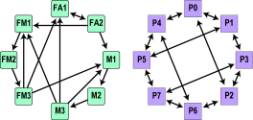
Figure 4. Parallelism in
Vector Processors and Ensembles
The vector processor in Figure 4 has a
3-stage floating-point multiplier (FM1, FM2, FM3), 2-stage floating-point adder (FA1, FA2),
and 3-stage memory unit (M1, M2, M3),
whereas the hypercube has processors P0 to P7. The vector processor has special
heterogeneous units with few options on the direction of output, whereas the
ensemble on the right has general homogeneous units with three possible outputs
from every unit. Nevertheless, both are parallel processors in the sense of
Amdahl’s Law: hardware is wasted whenever an algorithm cannot make use of all
the units simultaneously.
With the notable exceptions of the
NCUBE/ten hypercube (massively parallel but no vectors) and the Japanese
supercomputers (multiple pipelines but only one processor), virtually all
high-performance computers now make use of both
kinds of parallelism: vector pipelines and multiple processors. Examples
include the CRAY X-MP, ETA10, and FPS T Series. If we assume that Amdahl’s
argument applies to both techniques independently, then speedup is the product
of the parallel and vector speedups:
Speedup
= 1 ŕ [(s1 + p1 ŕ N1)(s2 + p2 ŕ N2)], (3)
where
s1 is the scalar fraction, p1
is the pipelined fraction, N1 is the vector
speedup ratio, s2 is the serial fraction, p2
is the parallel fraction, and N2 is the number of
processors. An example is shown in Figure 5 for the case of the
CRAY X–MP/4, where we estimate vector speedup N1 = 7.
The
figure makes near-optimal performance appear difficult to achieve. Even when
parallel and vector content are only 50% of the total, the speedup ranges only
from 7x to 11.2x. Now we apply the argument
of Section 3; the scaled speedup, assuming independence of vector and parallel
speedups, is
Speedup
= (s1 + N1p1)(s2 + N2p2), (4)
which
has the form shown in Figure 6.
The
speedup when parallel and vector content is 50% is now 16x to 17.5x,
considerably higher than before even for such small values of N1
and N2. It is much easier to approach the optimum
speedup of N1N2 than Amdahl’s
Law would imply.
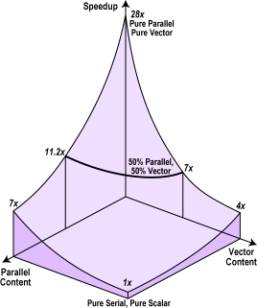
Figure
5. Parallel-Vector Speedup (Fixed-Sized Model)
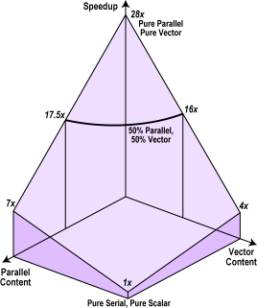
Figure
6. Parallel-Vector Speedup (Scaled Model)
6. Benchmarks
To
the best of the author’s knowledge, no widely-accepted computer benchmark
attempts to scale the problem to the capacity of the computer being measured.
The problem is invariably fixed, and then run on machines that range over
perhaps four orders of magnitude in performance.
A
well-known example is the LINPACK benchmark maintained by J. Dongarra of
Argonne National Laboratory [3]. The original form of the benchmark consisted
of timing the solution of 100 equations in 100 unknowns, single-precision or
double-precision, with or without hand-coded assembly language kernels. The
problem requires about 80 KBytes of storage and 687,000 floating-point
operations, and thus can be performed on even small personal computers (for
which the task takes two or three minutes). When run on a supercomputer such as
the CRAY X-MP/416 (8.5 nsec clock), the benchmark occupies only 0.06% of
available memory, only one of the four processors, and executes in 0.018
seconds (less time then it takes to update a CRT display). The resulting 39
MFLOPS performance is only a few percent of the peak capability of the
supercomputer, for reasons explainable by Amdahl’s Law.
It
seems extremely unrealistic to assume that a supercomputer would be used in
this way. Recognizing this, Dongarra has added 300-equation and 1000-equation
versions to his list, with dramatic effect on the observed performance. The
1000-equation benchmark uses 6% of the CRAY memory and requires 669 million
floating-point operations. With the problem so scaled, the solution requires
0.94 seconds, uses all four processors efficiently, and shows performance of
713 MFLOPS. It is fair to compare this with a scalar machine such as the VAX
8650 running the 100-equation problem, which takes about the same amount of
time (0.98 seconds) and yields 0.70 MFLOPS. Thus, it is fair to conclude that
the CRAY is 1020 times as fast as the VAX based on roughly constant-time
runs, which may be a more representative comparison than the ratio of 56 that
results from constant-sized problem runs.
Perhaps
one way to modify the LINPACK benchmark would be to solve the largest system of
equations possible in one second or less, and then use the
operation count to find MFLOPS. This allows a very wide range or performance to
be compared in a way more likely to correlate with actual machine use. In one
second, a personal computer with software floating-point arithmetic might solve
a system of 10 equations at a speed of about 0.0007 MFLOPS. In the same amount
of time, a supercomputer might solve a system of 1000 equations at a speed of
about 700 MFLOPS—a million times faster than the personal computer. The same
technique can be easily applied to any benchmark for which the problem can be
scaled and for which one can derive a precise operation count for the purpose
of computing MFLOPS.
7. Summary
When
comparing processor X to processor Y, it
is generally assumed that one runs the same problem on both machines and then
compares times. When this is done and X has far more
performance capability than Y as the result of
architectural differences (pipelines or multiple processors, for example), the
comparison becomes unrealistic because the problem size is fixed.
Because of the historical failure to recognize this, both vectorization and
massive parallelism have acquired the reputation of having limited utility as a
means of increasing computer power.
The seemingly disproportionate effect of
a small scalar or serial component in algorithms vanishes when the problem is scaled
and execution time is held constant. The functional form of Amdahl’s Law
changes to one in which the slow portion is merely proportional rather than
catastrophic in its effect. The constant-time paradigm is especially
well-suited to the comparison of computers having vastly different performance
capacities, as is usually the case when comparing highly-vectorized machines
with scalar machines, or massively-parallel machines with serial machines.
References
[1] Amdahl, G., “Validity of the Single-Processor
Approach to Achieving Large-Scale Computer Capabilities,” AFIPS Conference
Proceedings 30, 1967, pp. 483–485.
[2] Benner, R. E., Gustafson, J. L., and
Montry, G. R., “Development and Analysis of Scientific Applications Programs on
a 1024-Processor Hypercube,” SAND 88-0317, February 1988.
[3] Dongarra, J. J., “Performance of Various
Computers Using Standard Linear Equations Software in a Fortran Environment,” Technical
Memorandum No. 23, Argonne National Laboratory, October 14, 1987.