Reevaluating Amdahl's Law

John L. Gustafson

At Sandia National Laboratories, we are currently engaged in research involving massively-parallel processing. There is considerable skepticism regarding the viability of massive parallelism; the skepticism centers around Amdahl's law, an argument put forth by Gene Amdahl in 1967 [1] that even when the fraction of serial work in a given problem is small, say s, the maximum speedup obtainable from even an infinite number of parallel processors is only 1/s. We now have timing results for a 1024-processor system that demonstrate that the assumptions underlying Amdahl's 1967 argument are inappropriate for the current approach to massive ensemble parallelism.

If N is the number of processors, s is the amount of time spent (by a serial processor) on serial parts of a program and p is the amount of time spent (by a serial processor) on parts of the program that can be done in parallel, then Amdahl's law says that speedup is given by

Speedup = (s + p ) / (s + p / N )

= 1 / (s + p / N ),

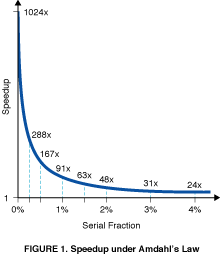
where we have set total time s + p = 1 for algebraic simplicity. For N = 1024, this is an unforgivingly steep function of s near s = 0 (see Figure 1).

The steepness of the graph near s = 0 (approximately - N2 ) implies that very few problems will experience even a 100-fold speedup. Yet for three very practical applications (s = 0.4 - 0.8 percent) used at Sandia, we have achieved the speedup factors on a 1024-processor hypercube which we believe are unprecedented [2]: 1021 for beam stress analysis using conjugate gradients, 1020 for baffled surface wave simulation using explicit finite differences, and 1016 for unstable fluid flow using flux-corrected transport. How can this be, when Amdahl's argument would predict otherwise?

The expression and graph both contain the implicit assumption that p is independent of N, which is virtually never the case. One does not take a fixed-size problem and run it on various numbers of processors except when doing academic research; in practice, the problem size scales with the number of processors. When given a more powerful processor, the problem generally expands to make use of the increased facilities. Users have control over such things as grid resolution, number of timesteps, difference operator complexity, and other parameters that are usually adjusted to allow the program to be run in some desired amount of time. Hence, it may be most realistic to assume that run time, not problem size, is constant.

As a first approximation, we have found that it is the parallel or vector part of a program that scales with the problem size. Times for vector startup, program loading, serial bottlenecks and I/O that make up the s component of the run do not grow with problem size. When we double the number of degrees of freedom in a physical simulation, we double the number of processors. But this means that, as a first approximation, the amount of work that can be done in parallel varies linearly with the number of processors. For the three applications mentioned above, we found that the parallel portion scaled by factors of 1023.9969, 1023.9965, and 1023.9965. If we use s' and p' to represent serial and parallel time spent on the parallel system, then a serial processor would require time s' + p' x N to perform the task. This reasoning gives an alternative to Amdahl's law suggested by E. Barsis at Sandia:

Scaled speedup = (s' + p' x N ) / (s' + p')
= s' + p' x N
= N + (1 - N ) x s'

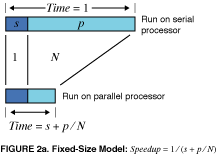
In contrast with Figure 1, this function is simply a line, and one with much more moderate slope: 1 - N. It is thus much easier to achieve efficient parallel performance than is implied by Amdahl's paradigm. The two approaches, fixed-sized and scaled-sized, are contrasted and summarized in Figure 2a and b.

Our work to date shows that it is not an insurmountable task to extract very high efficiency from a massively-parallel ensemble, for the reasons presented here. We feel that it is important for the computing research community to overcome the "mental block" against massive parallelism imposed by a misuse of Amdahl's speedup formula; speedup should be measured by scaling the problem to the number of processors, not fixing problem size. We expect to extend our success to a broader range of applications and even larger values for N.

REFERENCES

  1. Amdahl, G.M. Validity of the single-processor approach to achieving large scale computing capabilities. In AFIPS Conference Proceedings vol. 30 (Atlantic City, N.J., Apr. 18-20). AFIPS Press, Reston, Va., 1967, pp. 483-485.

  2. Benner, R.E., Gustafson, J.L., and Montry, G.R., Development and analysis of scientific application programs on a 1024-processor hypercube," SAND 88-0317, Sandia National Laboratories, Feb. 1988.