A LANGUAGE-INDEPENDENT SET OF BENCHMARKS FOR PARALLEL
PROCESSORS
John L. Gustafson and Stuart Hawkinson
Floating Point Systems, Inc.
September 9, 1986
Abstract
Benchmarks are essential for objective
comparison of computer performance. Established scientific computing benchmarks
(LINPACK, Whetstones, Livermore Kernels, etc.) are most appropriate for
sequential machines running Fortran. As architectures become increasingly
parallel, these benchmarks are decreasingly representative of the actual
performance achievable on large-scale scientific applications.
We present a set of six benchmarks that are
language-independent, representative of mainstream scientific computing, and
have parallel content approaching 100% as parameters grow large. They are
designed to fit a wide variety of multiprocessing approaches. The memory,
operation, and time complexity of each benchmark problem are analyzed. We
intend to promote collection and publication of performance figures for a large
set of both experimental and commercial computers, with strict controls to
insure integrity and verifiability of results.
Introduction
What makes a good benchmark? An examination of past
benchmarks [6, 8, 11, 12] suggests the following criteria:
1) It
should be representative of actual applications.
2) It
should not artificially exclude a particular architecture or configuration.
3) It
should reduce to a single number to
permit one-dimensional ranking.
4) It
should be large enough to exercise features of large machines, and be scalable
to smaller and larger versions.
5) It
should report enough details to be reproducible by an independent investigator.
6) It
should permit simple verification of the correctness of results.
7) It
should use algorithms simple enough to describe in about one page of text.
The ultimate goal of any benchmark is to estimate performance on an actual application of interest. Hence, the benchmark should be designed so that its one-dimensional ranking correlates well with a ranking of performance on the application. While this sounds like a nearly impossible task, benchmarks of scalar scientific computers have in fact historically been accepted as measures of application performance.
The requirement that a benchmark run on a variety of architectures and configurations has been neglected in many previous studies. The Whetstone benchmark [2], for example, is specifically designed to defeat attempts to vectorize, parallelize, or pipeline the code. Its operations are recursive, and hence measure only scalar performance. More recently, D. H. Bailey and J. T. Barton [1] have attempted to rectify this situation. Their NAS benchmarks provide seven Fortran kernels for vector uniprocessors and are intended to measure current supercomputer performance. The philosophy, however, is still one of minimum alteration to a specific Fortran formulation. Of the many parallel research machines recently funded by DARPA, not one is capable of illustrating its performance on the NAS benchmarks as stated. There obviously needs to be more flexibility in implementation if a performance metric is to have staying power.
The requirement that the benchmark reduce to a single
number is based on the historical misuse
of benchmarks. The Livermore Kernels [9] present an entire statistical base of
data, with 24 kernels run using three different mean vector lengths. Yet,
performance on those kernels is often stated as a single number, which might be
the harmonic mean or the arithmetic mean of various subsets of the data. It is
clear that computer performance is a multi-dimensional quantity, but in
practice, the metric inevitably becomes one-dimensional with repeated use. Even
the Whetstone benchmark was originally intended as a weighted mean of several
operations, with different sets of weights for different application mixes; yet
the only numbers ever used are the default weights suggested by Curnow and
Wichmann [2].
It is better for a benchmark problem to be too
large than too small. Ten years ago, solving 100 equations in 100 unknowns with
14-decimal accuracy seemed like a challenging computer task. On today’s
supercomputers, such a problem uses less than 1% of a machine’s main memory.
The problem has vectors too short to effectively amortize the cost of vector
startup in the arithmetic pipelines. Since applications have grown with the
available hardware, such a small problem is no longer representative of
large-scale scientific computation. Fortunately, the problem is easily scaled,
and solution times for 300-equation and 1000-equation systems are beginning to
be quoted [3]. Dense systems as large as 25000 by 25000 have been recently run
as performance tests at Floating Point Systems.
Benchmarks are experiments, subject to the same
control requirements as any other scientific experiment. A measurement of a
computing system must be accompanied by
considerable supporting information, such as:
1) Numerical
format used (mantissa size, exponent size)
2) Operating
system release level
3) Language
and release level; directives and options used
4) Memory
size, cache, mass storage, and any other variable storage information
5) Number of processors, interprocessor communication speeds, processor clock speeds, and any other physical variables of the configuration
6) Date
run
7) Who
performed the measurement, and how that person can be contacted
These requirements are a bare minimum for
reproducibility in the experiment. It is assumed that no other users are
present on a computer system running a benchmark problem, and that times quoted
are always elapsed times rather than “CPU time” or other subset of the
computing resource. Perhaps the most important item in the above list is the
name of the person who performed the benchmark. Too often, published benchmarks
use anonymous sources, which reduces the traceability of the results. Ideally,
results should be gathered and maintained by an independent national agency;
the National Bureau of Standards has already expressed interest in taking on
this responsibility [10]
The ease-of-verification requirement is
obvious. If one does not require that programs run correctly, then one can make them run very quickly indeed. We take
the view that the person who programs the benchmark for a particular machine is
responsible for making certain that the program actually does the stated job.
While verification facilities can be provided in the program, a person
motivated to circumvent them will probably never have the least bit of trouble
doing so. Proof of correctness should be viewed similarly to the requirement
for correctness in published mathematical proofs; testing a theorem by example
might weed out an error, but can never prove correctness.
Finally, the algorithms describing the benchmark problems
should be describable in about one page of text. Benchmarks are often
criticized as being too short to represent very large application programs, and
this is particularly valid if one is measuring a machine with a program cache.
The tradeoff is that long benchmarks are generally much harder to convert to
various machines, greatly reducing the eventual database of the benchmark. John
Swanson has collected a sizeable list of computer performance on his ANSYS®
structural analysis code (over 150,000 lines of Fortran), but only within the
realm of sequential Fortran processors. Swanson’s measurements are among the
best, however, for revealing overall system performance on a large Fortran
program. In general, however, a small set of short kernels can be
representative of overall performance in scientific applications; we make the
tradeoff in the direction of simplicity because of the desire for language
independence.
An excellent example of a language-independent
benchmark in wide use is the Fast Fourier Transform. It is usually cited for
either a 1024-point linear array, or the two-dimensional transform of a 1024 by
1024-point array of complex numbers. Although it is generally not specified
whether the data is left bit-reversed or in correct order, the FFT benchmark
needs no statement about specific data, language, number of processors, etc.
The correctness of the program is easily checked by applying the inverse FFT
and comparing with the original data. It conveys speed on a problem of intense
interest to certain applications. This is the paradigm for our six benchmark
problems.
We have selected six problems that represent a
cross-section of scientific computing:
1) Matrix
Multiplication
2) Wave
Equation
3) Linear
System Solution
4) Two-Dimensional
Convolution
5) Two-Dimensional
Discrete Fourier Transform
6) Three-Dimensional
N-Body Simulation
As typified by the FFT, each benchmark is
described as a mathematical task to be
performed, with plenty of freedom to allow a programmer to use a particular
machine to good advantage. For clarity, we supply a sample implementation in
Fortran. The problem is analyzed for memory complexity, operation complexity,
time complexity, theoretical maximum parallelism in the flow of data, what
architectural features are being exercised, and what applications correlate
well with the problem.
Each Fortran listing is intended only as an
explanation of the problem being solved, not as a specification of the order of
computations. The authors have little interest in knowing how cleverly an
optimizing Fortran compiler can reconstruct parallelism from the serialized
versions shown here. Data are generated with a system-supplied function “RAN(ISEED)” which delivers a pseudo-random sequence of real values
uniformly distributed between 0 and 1. It may be assumed that the data do not
produce underflow, overflow, or division by zero. The Fortran examples use a
system call “SECONDS(T1)” which returns the
absolute “wall clock” time in T1; this can then be used
to compute elapsed time.
Storage required, or “memory complexity,” is stated as an asymptotic term which ignores lower-order terms and scratch usage. It also does not account for the possible need for redundant storage on multiple processors.
“Operation complexity” refers to the total
number of floating-point operations required by the algorithm. “Time
complexity” refers to the number of operations in the critical path of the data
dependency graph. Execution time on a serial computer will depend mostly on
operation complexity; execution time on a highly parallel computer will depend
mostly on time complexity. With the exception of the industry-standard 1K by 1K
FFT, the parameters have been chosen so that the benchmarks have operation
complexities of approximately one billion. We use the operation weighting
suggested by McMahon [9]:
Operation Complexity
Add, subtract, compare 1
Multiply 1
Reciprocal 3
Square root 4
“Maximum parallelism” describes the breadth of
the data dependency graph, that is, the maximum concurrency that can be
exploited in the algorithm. The algorithms all have maximum parallelism in
excess of 106 using the suggested parameters, so that even massively
parallel designs will be able to demonstrate performance improvements.
BENCHMARKS
Implementation Notes:
All floating-point numbers are assumed to have
a dynamic range of at least 10–300 to 10+300 and at least
15 decimal digits of mantissa precision. All computers with hardware or
software based on the IEEE proposed 64-bit floating-point standard meet this
requirement. A complex number consists of two such floating-point numbers and
thus requires at least 128 bits. A “word” is a unit of storage with at least 64
bits.
Timing begins when the first calculation is
performed on input data (not parameters). It ends when the last necessary
calculation is finished. The data can be stored wherever convenient before
starting the timer (registers, caches, multiple local memories, etc.) Timing
should not include the time required to fill the arrays with starting data,
even if data is stored redundantly on multiple processors. The data may be
stored in any regular order required for maximum performance. Precomputing
results or partial results is not permitted unless specifically stated in the
problem description.
The “single number” quoted for this suite of
six benchmarks is the sum of the six individual timings. Equivalently, one may
compute total MFLOPS as the total number of floating-point operations
(operation complexity) divided by the total number of microseconds of elapsed
time, if care is taken to consider only those MFLOPS essential to the
computation. (A driver program is being developed to implement these guidelines
and execute the six benchmarks. It will produce a table of required information
and a summary of results.)
1) MATRIX MULTIPLICATION
Given N-by-N 64-bit floating-point matrices A and B,
compute the matrix product C = AB. All matrices are considered dense and asymmetric.
Sample parameter: N = 1024.
Fortran sample implementation:
C
Problem 1: Matrix Multiplication
JLG 3/14/86
C
PARAMETER (N=1024)
REAL A(N,N), B(N,N), C(N,N)
C
C
Set up matrix data.
C
ISEED = 31415
DO 1 I = 1, N
DO 1 J = 1, N
A(I,J) =
RAN(ISEED)
1 B(I,J) = RAN(ISEED)
C
C
Start timer and begin computation.
C
CALL SECONDS(T1)
DO 2 I = 1, N
DO 2 J = 1, N
SUM = A(I,1)
* B(1,J)
DO 3 K = 2,
N
3 SUM = SUM +
A(I,K) * B(K,J)
2 C(I,J) = SUM
C
C
Finished; stop timer.
C
CALL SECONDS(T2)
WRITE(6,*) ' Elapsed time in
seconds:', T2 - T1
STOP
END
Memory complexity:
Approximately 2N 2
words (by replacing A or B with the result C). (For N = 1024,
this is 2.1 million words, or 17 million bytes).
Operation complexity: N 3
multiplications, N 3 – N 2 additions; 2N 3 – N 2 total floating-point operations. (For N = 1024, this is 2.1464 billion floating-point operations.)
Time complexity: 1 multiplication and lg N additions (see Figure 1.) (For N = 1024, this is 11 operations.)
Maximum parallelism: N 3
multiplications. (For N = 1024,
this is 1.1 billion.)
Matrix multiplication should
execute at very close to “peak theoretical speed” on most scientific computers.
The ratio of floating-point multiplications to additions is nearly unity, which
corresponds to a common design ratio of one adder functional unit to every
multiplier functional unit. This benchmark tests ability to use arithmetic
units with a minimum of communication overhead; each word of input data is used
in N operations. Systolic algorithms
using a two-dimensional mesh of processors are well known [7]; the diagram
below suggests that logarithmic interconnectivity can further reduce execution
time.
Matrix multiplication is essential for
similarity transformations and certain kinds of eigenvalue-eigenvector
computation. Computational chemistry depends heavily on matrix multiplication
for ab initio modeling of molecular
behavior.
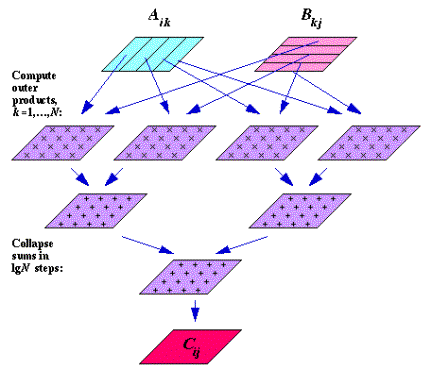
Figure 1. Parallel Matrix Multiplication
2) WAVE EQUATION
Simulate the wave equation on the interior of
an N-by-N grid of points. Follow the progress of the wave through T time steps.
Two time steps, U(i, j) and V(i, j), are initialized
before timing starts. The boundaries of the grids are initialized to zero, and
are never updated. The interiors are initialized to dense sets of
floating-point numbers.
The simulation uses an
explicit time stepping scheme:
U(i, j ) ¬ [V(i + 1, j) + V(i – 1, j)
+ V(i, j + 1) + V(i, j – 1)] ę 0.5 – U(i, j)
for
2 ≤ i, j ≤ N – 1,
followed by
V(i, j ) ¬ [U(i + 1, j) + U(i – 1, j)
+ U(i, j + 1) + U(i, j – 1)] ę 0.5 – V(i, j)
for 2 ≤ i , j ≤ N – 1. Each update of U and then V
counts as two time steps. Only the last two time steps are to be saved.
Sample parameters: N=1024, T=250.
Fortran sample implementation:
C
Problem 2: Wave Equation JLG 3/14/86
C
PARAMETER (N = 1024, N2 = N/2, ITIME
= 250)
REAL U(N,N), V(N,N)
C
C
Initialize the time steps.
C
ISEED = 31415
DO 1 I = 1, N
DO 1 J = 1, N
U(I,J) =
RAN(ISEED)
1 V(I,J) = RAN(ISEED)
U(N2,N2) = 100.0
C
C
Start the timer and begin computing.
C
CALL SECONDS(T1)
DO 2 NT = 1, ITIME - 1, 2
DO 3 I = 2, N-1
DO 3 J = 2,
N-1
U(I,J) = (V(I+1,J)+V(I-1,J)
$
+ V(I,J+1)+V(I,J-1))*0.5 - U(I,J)
3 CONTINUE
DO 4 I = 2, N-1
DO 4 J = 2,
N-1
V(I,J) = (U(I+1,J)+U(I-1,J)
$ +
U(I,J+1)+U(I,J-1))*0.5 - V(I,J)
4 CONTINUE
2
CONTINUE
C
C
Finished; stop timer.
C
CALL SECONDS(T2)
WRITE(6,*) ' Elapsed time in
seconds:', T2 - T1
STOP
END
Memory complexity: Approximately
2N 2 words. (For N = 1024, this is 2.1 million words, or 17 million
bytes.)
Operation complexity: 4(N – 2)2T additions, (N – 2)2T multiplications; 5(N – 2)2T total floating-point operations. [By re-using sums, the additions can
be reduced to 3(N – 2)2T at the expense of reducing the maximum parallelism
somewhat. In this case, use 4(N –2)3T to compute MFLOPS ratings from this benchmark. (For N = 1024 and T = 250, this is 1.0445 billion floating-point
operations.)]
Time complexity: 3T additions and T multiplications. (See Figure 2). (For T = 250, this is 1000 operations.)
Maximum parallelism: 2N2
additions at the beginning of every time step. (For N = 1024, this is 2.1 million.)
This benchmark is memory/communication
intensive, since each word of data communicated between neighboring points only
participates in a single calculation. However, the method is highly parallel
because of the explicit formulation, which can exercise a large number of
processors running similar programs.
The wave equation is one of the most important equations of mathematical physics. It is used by the seismic industry to simulate various exploration strategies, sometimes using formulations scarcely more complicated than the one used here. Fluids can be modeled by similar methods when their behavior is wavelike (hyperbolic), such as in transonic flow.
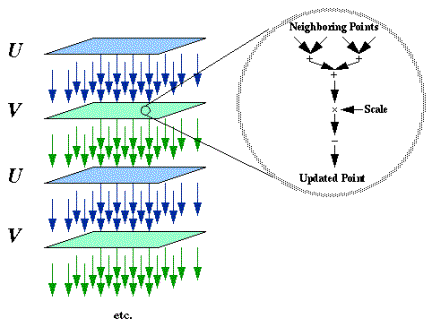
Figure 2. Parallel Wave Equation Simulation
3) LINEAR SYSTEM SOLUTION
Given an N-by-N floating-point matrix A
and an N-long floating-point vector b, find an N-long
floating-point vector x such
that Ax = b. All matrices and vectors are assumed dense. The matrix A is real, asymmetric, and nonsingular.
Use any method with numerical error equal to or
less than that of Gaussian elimination with partial pivoting. For example, one
might use LU factorization with
pivoting, then forward reduction, and then backsolving, or one might combine
passes by using Gauss-Jordan elimination with pivoting. Pivoting must be across
all non-eliminated columns, not just those local to a processor. A and b may
be altered in the process of solution; only x is required as output.
Sample parameters: N = 1023. (This allows the augmented matrix to have a
width of 1024 elements.)
Fortran sample implementation:
C
Problem 3: Linear System Solution
JLG 1/27/86
C
PARAMETER (N = 1023)
REAL A(N,N+1), X(N), R(N)
EQUIVALENCE (A(1,N+1), X(1))
C
C
Set up matrix and vector data.
C
ISEED = 31415
DO 1 I = 1, N
DO 1 J = 1, N + 1
1 A(I,J) = RAN(ISEED)
C
C
Start timer and begin computation.
C
CALL SECONDS(T1)
DO 2 K = 1, N - 1
S = ABS(A(K,K))
L = K
DO 3 I = K + 1, N
IF (S .GE.
ABS(A(I,M))) GO TO 3
S =
ABS(A(I,M))
L = I
3 CONTINUE
DO 4 I = K, N
S = A(K,I)
A(K,I) = A(L,I)
4 A(L,I) = S
R(K) = 1.0 / A(K,K)
DO 5 I = K + 1, N
S = A(I,K) *
R(K)
DO 5 J =
K+1, N+1
5 A(I,J) =
A(I,J) - S * A(K,J)
2
CONTINUE
R(N) = 1.0 / R(N)
C
C
Backsolve...
C
X(N) = X(N) * R(N)
DO 6 I = N - 1, 1, -1
DO 7 J = I + 1, N
7 X(I) = X(I) - X(J) *
A(I,J)
6 X(I) = X(I) * R(I)
C
C
Finished; stop timer.
C
CALL SECONDS(T2)
WRITE(6,*) ' Elapsed time in
seconds:', T2 - T1
STOP
END
Memory complexity: N2 words. (For N = 1023, this is 1 million words, or 8.4 million
bytes.)
Operation complexity:
1ŕ3N 3 + N 2 – 1ŕ3N additions (including comparison operations), 1ŕ3N 3
+ N 2 – 1ŕ3N multiplications,
and N reciprocals; 2ŕ3 N 3 + 2N 2 + 7ŕ3 N total floating-point operations. (For N = 1023, this is 0.7158 billion floating-point
operations.)
Time complexity: (lg N)(N+1) + 2N – 1 additions, 3N – 1 multiplications, and N reciprocals. (For N = 1023, time complexity is about 20000.)
Maximum parallelism: (N – 1)2 multiplications and additions after
the first pivot element is found. (For N = 1023, this is about 1 million.)
Linear equations solving has
a kernel that resembles matrix multiplication; however, the need to choose a
pivot value introduces a major change for parallel computation. There is much
more time complexity in Gaussian Elimination than in matrix multiplication,
although each word of data participates in roughly the same number of
calculations. The backsolving step tends to be communication-bound.
Direct solvers are essential in several
applications. Structural analysis uses direct solution on matrices with
envelope sparsity; within the envelope, the operation resembles the problem
described above. Integral formulations of boundary value problems (such as
those used for determining radar cross-section) require direct solution of
dense systems. In general, implicit formulations of physical problems result in
a need to solve systems of simultaneous equations.
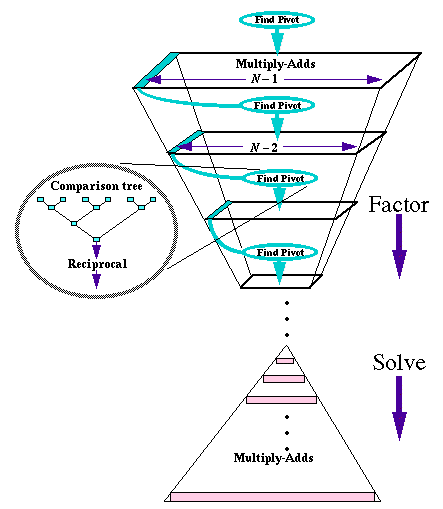
Figure 3. Parallel Gaussian Elimination
4) TWO-DIMENSIONAL CONVOLUTION
Given an image A and an M-by-M filter F,
compute an N-by-N array B, the
convolution of A with F. Compute only that subset such that the filter does not
extend beyond the edge of the image; hence A must have dimensions N + M – 1
by N + M – 1. The convolution is defined as
for i, j = M + 1
to N + M. Only B needs
to be saved.
Sample parameters: N = 1024,
M = 25.
Fortran sample implementation:
C
Problem 4: Two-Dimensional Convolution JLG 3/14/86
C
PARAMETER (N = 1024, M = 25)
DIMENSION A(N+M-1,N+M-1), B(N,N),
F(M,M)
C
C
Set up image and filter data.
C
ISEED = 31415
DO 1 I = 1, N+M-1
DO 1 J = 1, N+M-1
1 A(I,J) = RAN(ISEED)
DO 2 I = 1, M
DO 2 J = 1, M
2 F(I,J) = RAN(ISEED)
C
C
Start timer and begin computation.
C
CALL SECONDS(T1)
DO 3 I = M + 1, N + M
DO 3 J = M + 1, N + M
SUM = 0.0
DO 4 K = 1,
M
DO 4 L = 1, M
4
SUM = SUM + A(I-K,J-L) * F(K,L)
3 B(I-M,J-M) = SUM
C
C
Finished; stop timer.
C
CALL SECONDS(T2)
WRITE(6,*) ' Elapsed time in
seconds:', T2 - T1
END
Memory complexity: Approximately 2N 2 words. (For N = 1024, this is 2.1 million words, or 16.8 million
bytes.)
Operation complexity: N 2(M 2 – 1) additions and N 2M 2
multiplications; N 2(2M 2 – 1) total floating-point
operations. (For N = 1024 and
M = 25, this is 1.3097
billion operations.)
Time complexity: 2 lg M additions
and 1 multiplication. (See Figure 4.) (For M = 25, this is 11 operations)
Maximum parallelism: N 2M 2 multiplications in the first step. (For N = 1024 and M = 25, this is 655 million.)
This function differs from matrix
multiplication in its pattern of re-use of data. The filter data is re-used
intensively and can be broadcast for effective parallelization.
Convolution is the most important time-domain operation in signal and image processing. When filters become larger than about 64 elements in any dimension, FFT methods are more efficient. Convolution strongly resembles the fundamental operation of finite-difference iterative methods, applying an inner-product operator to a local subset of the data to “relax” toward a solution. Hence, performance on this benchmark should correlate strongly with performance on certain partial differential equation methods.
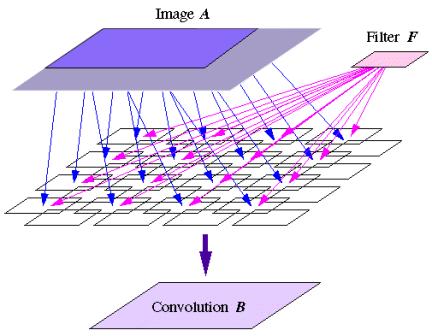
Figure 4. Parallel Two-Dimensional Convolution
5) TWO-DIMENSIONAL DISCRETE FOURIER
TRANSFORM
Given an N-by-N image A consisting of complex pairs of floating-point numbers,
compute its two-dimensional Discrete Fourier Transform B, followed by its scaled inverse C, which should reproduce the original image A. The transform is defined as
for k, l = 0, … , N – 1; its inverse is defined as
![]()
for m, n = 0, …, N – 1, where w = e –2Ļi ŕ N.
FFT methods may be used,
either in-place or out-of-place. Only C must be saved;
timing ends when it is stored in the original order used to store A. Do not include time to prepare sine and cosine tables.
Sample Parameter: N = 1024
Fortran sample implementation (see [1]):
C
Problem 5: Two-Dimensional Discrete Fourier Transform
C
(using radix 2 FFT methods)
JLG 1/26/86
C
PARAMETER (N = 1024, N2 = N/2)
COMPLEX A(N,N), W(N)
INTEGER IP(2,N)
C
C
Initialize trig tables and input data.
C
ISEED = 31415
DO 1 I = 1, N2
T = 2. *
3.141592653589793 * (I-1) / N
1 W(I) = CMPLX(COS(T), SIN(T))
DO 2 I = 1, N
DO 2 J = 1, N
2 A(I,J) = RAN(ISEED)
SCALE = 1. / FLOAT(N * N)
C
C
Start timer and begin computation.
C
CALL SECONDS(T1)
CALL FFT(A,N,W,IP,+1)
CALL TRANS(A,N)
CALL FFT(A,N,W,IP,+1)
DO 3 I = 1, N
DO 3 J = 1, N
3 A(I,J) = A(I,J) * SCALE
CALL FFT(A,N,W,IP,-1)
CALL TRANS(A,N)
CALL FFT(A,N,W,IP,-1)
C
C
Finished; stop timer.
C
CALL SECONDS(T2)
WRITE(6,*) ' Elapsed time in
seconds:', T2 - T1
STOP
END
C
C
Compute 1D FFTs (based on routine by D.H. Bailey):
C
SUBROUTINE FFT(A,N,W,IP,IFLAG)
COMPLEX A(N,N), W(N), CX, CT
INTEGER IP(2,N)
DO 4 I = 1, N
4 IP(1,I) = I
L = 1
K1 = 1
5 K2
= 3 - K1
N2 = N/2
DO 6 J = L, N2, L
CX = W(J-L+1)
IF (IFLAG .LT. 0) CX =
CONJG(CX)
DO 6 I = J-L+1, J
II =
IP(K1,I)
IP(K2,I+J-L)
= II
IM =
IP(K1,I+N2)
IP(K2,I+J) =
IM
DO 6 K = 1,
N
CT = A(II,K) - A(IM,K)
A(II,K) = A(II,K) + A(IM,K)
6 A(IM,K) = CT
* CX
L = 2 * L
K1 = K2
IF (L .LE. N2) GO TO 5
DO 7 I = 1, N
II = IP(K1,I)
IF (II .LE. I) GO TO 7
DO 8 K = 1,
N
CT = A(I,K)
A(I,K) =
A(II,K)
8 A(II,K) = CT
7 CONTINUE
RETURN
END
C
C
Transpose complex array in place.
C
SUBROUTINE TRANS(A,N)
COMPLEX A(N,N), CT
DO 9 I = 1, N - 1
DO 9 J = I + 1, N
CT = A(I,J)
A(I,J) =
A(J,I)
9 A(J,I) = CT
RETURN
END
Memory complexity: Approximately
2N 2. (For N = 1024, this is about 2.1 million words, or 16.8
million bytes.)
Operation complexity: If radix 2 FFT methods are used, there are 12 N 2 lg N additions and N 2(8 lg N + 2) multiplications; N 2(20 lg N + 2) total floating-point operations. This is not the theoretical minimum number of operations; however, use
N 2(20 lg N + 2) to compute MFLOPS ratings for this
benchmark. (For N = 1024,
this is 0.2118 billion floating-point operations).
Time complexity: 4 lg N + 1 multiplications and 8 lg N additions, for the radix 2 FFT. (For N = 1024, this is 121 operations).
Maximum parallelism: 8N 2 multiplications in the beginning of each radix
2 FFT. (For N=1024, this is 8.4
million.)
A number of multiprocessor connection schemes
are appropriate for the FFT: hypercube, omega network, and butterfly, for
example. Nearest-neighbor schemes in two or three dimensions do not have
adequate direct interconnects for most factorings of the Discrete Fourier
Transform.
Besides the obvious importance of discrete Fourier Transforms in signal and image processing performing convolutions or extracting frequency spectra, they are essential for spectral methods used in mathematical physics. Computational fluid dynamics, notably weather modeling, sometimes uses FFTs to convert space-domain problems into more easily solved frequency-domain problems.
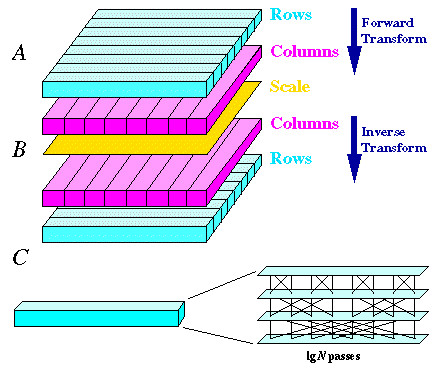
Figure 5. Parallel Two-Dimensional FFT
6) THREE-DIMENSIONAL N-BODY SIMULATION
Simulate the time evolution of a system of N point masses with Newtonian gravitational forces in three
spatial dimensions; that is, the force between any two bodies mi and mj
is described by
Fij = –Gmimj rij ŕ || rij ||3
where G is the
gravitational constant and rij is the vector from mass i to mass j. For
simplicity, we assume that G = 1
and mi = 1 for i = 1, … , N. Hence the total force on body mi is
![]()
Assume an initial set of nonzero velocities vi. Use a
simple time stepping method [4] to update velocities and positions, with T time steps of size h.
Compute Fi for i = 1, … , N. Then new velocities viĘ and riĘ are obtained from vi and ri using
viĘ = vi + h Fi
riĘ = ri + h viĘ
for i = 1, … , N. Repeat for T time
steps. Note that cluster approximations, which replace groups of particles with
a point mass, are not permitted.
Sample parameters: N = 1024, T = 50,
h = 0.0001
Fortran sample implementation:
C
Problem 6: N-Body Simulation
JLG 3/14/86
C
PARAMETER (N = 1024, ITIME = 50, H =
0.0001)
DIMENSION
R(N,3),R1(N,3),V(N,3),V1(N,3),FORCE(3),DEL(3)
C
C
Set up initial positions and velocities.
C
ISEED = 31415
DO 1 I = 1, N
DO 1 J = 1, 3
R(I,J) =
RAN(ISEED)
1 V(I,J) = RAN(ISEED)
C
C
Start timer and begin computation.
C
CALL SECONDS(T1)
DO 2 NT = 1, ITIME
DO 3 I = 1, N
DO 4 IDIM =
1, 3
4 FORCE(IDIM)
= 0.0
DO 5 J = 1,
N
IF (I .EQ. J) GO TO 5
DO 6 IDIM = 1,3
6
DEL(IDIM) = R(I,IDIM) - R(J,IDIM)
RIJ = DEL(1)**2 + DEL(2)**2 + DEL(3)**2
RIJ = 1. / (RIJ * SQRT(RIJ))
DO 5 IDIM = 1, 3
FORCE(IDIM)=FORCE(IDIM)+DEL(IDIM)* RIJ
5 CONTINUE
DO 7 IDIM =
1, 3
V1(I,IDIM) = V(I,IDIM) + FORCE(IDIM) * H
7 R1(I,IDIM) =
R(I,IDIM) + V1(I,IDIM) * H
3 CONTINUE
DO 8 I = 1, N
DO 8 IDIM =
1, 3
V(I,IDIM) = V1(I,IDIM)
8 R(I,IDIM) =
R1(I,IDIM)
2
CONTINUE
C
C
Finished; stop timer.
C
CALL SECONDS(T2)
WRITE(6,*) ' Elapsed time in seconds:',
T2 - T1
END
Memory complexity: 12N words. (For N = 1024,
this is 12 Kwords, or 100 Kbytes).
Operation complexity: (8N 2 – 2N)T additions, (7N 2 – N)T multiplications,
(N 2 – N)T square roots,
and (N 2 – N)T reciprocal
operations; (22N 2 – 10N)T total
floating-point operations. (For N = 1024
and T = 50, this is 1.1538
billion operations.)
Time complexity: 6T
additions, 5T multiplications, T square
roots, and T reciprocals. (For T = 50, this is 90 operations.)
Maximum Parallelism: 3(N 2 – N) additions at the beginning of each time step. (For N = 1024, this is 3.1 million.)
A discussion of this problem and its fit to parallel architectures can be found in [5]. In general, ring interconnectivity is sufficient to achieve high parallel performance, despite the apparently high everything-to-everything costs. Plasma simulation and astrophysical simulations illustrate the range of applicability of such algorithms.
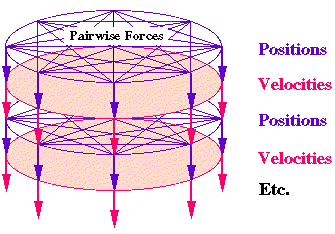
Figure 6. Parallel N -Body Simulation
SUMMARY
The suite of six benchmarks presented in this paper is designed to measure the performance of parallel scientific computers. They are sufficiently general to permit various architectures to achieve a high percentage of their optimum performance. No artificial restrictions have been placed on language, evaluation order, or parallelism. The Fortran listings are meant only to clarify the computations required and serve as an independent source of results for testing. The size of each benchmark has been adjusted so that each kernel makes a significant contribution to the total execution time.
The following table summarizes the six benchmarks for the
sample parameters:
Benchmark Memory, Billions
of Minimum Max. Parallelism,
Megabytes Operations Time Millions
Matrix Multiplication 17. 2.1464 11 1074.
Wave Equation 17. 1.0445 1000 2.1
Linear Equations 8.4 0.7158 20000 1.
Convolution 17. 1.3097 11 655.
2D Fourier Transform 17. 0.2118 121 8.4
N-Body
Simulation 0.1 1.1538 90 3.1
The guidelines presented should allow the reported benchmark results to be analyzed, understood, and repeated. It is hoped that these kernel computations will be run on many new parallel architectures regardless of language, task granularity, or memory organization. The authors would appreciate reports of any results and will promote their discussion to as wide an audience as possible.
REFERENCES
[1] Bailey,
D. H., and Barton, J. T., “The NAS Kernel Benchmark Program,” NASA Technical
Memorandum 86711, (August 1985).
[2] Curnow,
H. J., and Wichmann, B. A., “A Synthetic Benchmark,” Computer Journal, 19, 1, (February
1976).
[3] Dongarra,
J. J., “Performance of Various Computers Using Standard Linear Equations
Software in a Fortran Environment,” ANL Technical Memorandum 23, (November
1985).
[4] Feynman,
R.P., The Feynman Lectures on Physics,
Vol. I, Addison Wesley, (1964), 9–5 to 9–9.
[5] Fox,
G. C., and Otto, S. W., “Algorithms for Concurrent Processors,” Physics
Today, (May 1984), 50–59.
[6] Gustafson,
J. L., “Measuring MFLOPS,” Floating Point Systems Application Note #52, (June 1985).
[7] Kung,
H.T., “Why Systolic Architectures,” IEEE Computer, 15, 1, (January
1982), 37–46.
[8] Marvit,
P., and Nair, M, “Benchmark Confessions,” BYTE, 9, 2, (February
1984), 227–230.
[9] McMahon,
F. H., “L.L.N.L FORTRAN KERNELS: MFLOPS,” Lawrence Livermore National
Laboratory, (benchmark tape available), (1983).
[10] National Bureau
of Standards Announcement, “NBS Parallel Computer Benchmark Collection,” J.
Comp. Physics, 61, (1985), 523.
[11] Purdom, J., “Benchmark Philosophy and Methodology,” Computer
Language, 3, 2, (February, 1986), 49–56.
[12] Worlton, J., “Understanding Supercomputer Benchmarks,” Datamation, (September 1, 1984), 121–130.